题目内容
已知：在梯形ABCD中，AD∥BC，∠B＝∠C(如图)．
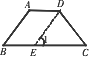
求证：AB＝DC．
答案：
解析：
解析：
|
转化方法1：平移一腰 证法1：如图，过点D作DE∥AB，交BC于点E．
所以∠B＝∠1．又∠B＝∠C，所以∠C＝∠1．所以DE＝DC．又AB∥DE，AD∥BE，所以四边形ABED为平行四边形．所以AB＝DE．所以AB＝DC． 转化方法2：延长两腰 证法2：如图，分别延长BA、CD，交于点E．
因为∠B＝∠C，所以BE＝CE． 因为AD∥BC，所以∠B＝∠1，∠C＝∠2．所以∠1＝∠2．所以AE＝DE．所以BE－AE＝CE－DE，即AB＝DC． 转化方法3：作高转化 证法3：如图，分别过A、D两点作AE⊥BC，DF⊥BC，垂足分别为点E、F，所以AE∥DF．
又因为AD∥BC，所以四边形AEFD为矩形． 所以AE＝DF． 在Rt△ABE和Rt△DCF中，因为∠B＝∠C，∠AEB＝∠DFC＝90°，AE＝DF， 所以Rt△ABE≌Rt△DCF(AAS)．所以AB＝DC． |
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
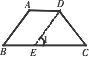
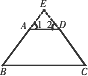
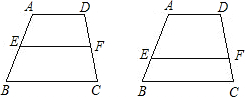已知：在梯形ABCD中，AD∥BC，点E在AB上，点F在DC上，且AD=a，BC=b．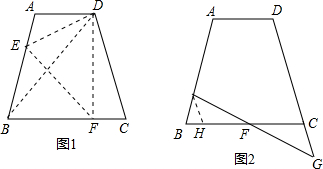
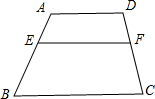如图，已知：在梯形ABCD中，AD∥BC，AD=3，BC=5，点E在AB上，且AE：EB=2：3，过点E作EF∥BC交CD于F，求EF的长？
已知：在梯形ABCD中，AD∥BC，AB=DC=5，AD=3.5，
已知，在梯形ABCD中，AD∥BC，∠ABC=90°，BC=2AD，点E、F分别是BC和DC的中点，连接AE、EF和BD，AE和BD相交于点G．