题目内容
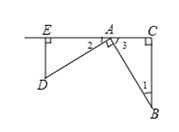
【题目】（1）己知：如图，△ABC，∠C=90°，现将斜边AB绕A点顺时针旋转90°到AD，过D点作DE⊥CA，交CA的延长线于点E.求证：△ABC ≌ △DAE
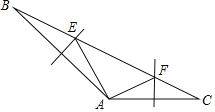
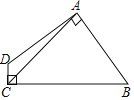
（2）如图，四边形ABCD中，AB=AD，AC=5，∠DAB=∠DCB=90°，则四边形ABCD的面积为 。
【答案】（1）见解析（2）
【解析】
（1）根据垂直的性质得到∠1=∠2，，利用AAS即可证明△ABC ≌ △DAE；
（2）过A点作BC的垂直交于E,过点A作CD的延长线于点F，根据（1）可知△AFD≌△AEB，故四边形ABCD的面积等于正方形AECF的面积，再根据AC为对角线即可求解.
（1）∵将斜边AB绕A点顺时针旋转90°到AD，
∴∠BAD=90°，AD=AB
∠2+∠3=90°，
∵∠C=90°
∴∠1+∠3=90°，
∴∠1=∠2，
又DE⊥CA
∴△ABC ≌ △DAE（AAS）
（2）过A点作BC的垂直交于E,过点A作CD的延长线于点F，
∵∠DAB=∠DCB=90°=∠F，
四边形AECF为矩形，
∵AB=AD，∠DAB=90°，
根据（1）可知△AFD≌△AEB，
∴AF=AE，
∴矩形AECF为正方形，
由△AFD≌△AEB
∴四边形ABCD的面积等于正方形AECF的面积，
∵AC是正方形AECF的对角线，
∴S正方形AECF=
×AC2=
故四边形ABCD的面积等于.
练习册系列答案
阅读快车系列答案
相关题目
