题目内容
【题目】如图,已知△ABC中,边AB、AC的垂直平分线分别交BC于E、F,若∠EAF=90°,AF=3,AE=4.
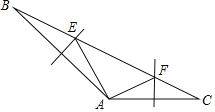
(1)求边BC的长;(2)求出∠BAC的度数.
【答案】(1)BC=12;(2)∠BAC=135°.
【解析】
(1)根据勾股定理求出EF,根据线段垂直平分线的性质得到EA=EB,FA=FC,结合图形计算,得到答案;
(2)根据等腰三角形的性质得到∠EAB=∠B,∠FAC=∠C,根据三角形内角和定理计算即可.
解:(1)由勾股定理得,EF=![]() =
=![]() =5,
=5,
∵边AB、AC的垂直平分线分别交BC于E、F,
∴EA=EB,FA=FC,
∴BC=BE+EF+FC=AE+EF+AF=12;
(2)∵EA=EB,FA=FC,
∴∠EAB=∠B,∠FAC=∠C,
由三角形内角和定理得,∠EAB+∠B+∠EAF+∠FAC+∠C=180°,
∴∠B+∠C=45°,
∴∠BAC=180°﹣∠B﹣∠C=135°.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目