题目内容
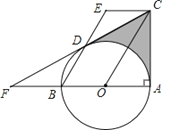
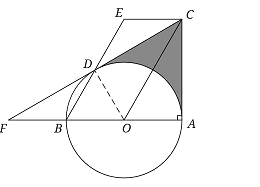
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
【答案】(1)证明见解析;(2)S阴=4![]() ﹣
﹣![]() .
.
【解析】试题(1) 根据两直线平行,同位角相等,内错角相等,证明![]() ,利用全等三角形“SAS”判定定理,证明
,利用全等三角形“SAS”判定定理,证明![]() ,得到OD⊥CD,所以CF为⊙O的切线.
,得到OD⊥CD,所以CF为⊙O的切线.
(2) 利用三角函数和角度的关系,计算出OA,OC的长度和∠DOA的度数,分别求出四边形OACD和扇形OAD的面积,相减即可得到阴影部分的面积.
试题解析:(1)证明:如图连接OD.
∵四边形OBEC是平行四边形,
∴OC∥BE,
∴∠AOC=∠OBE,∠COD=∠ODB,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠DOC=∠AOC,
在△COD和△COA中,
 ,
,
∴△COD≌△COA,
∴∠CAO=∠CDO=90°,
∴CF⊥OD,
∴CF是⊙O的切线.
(2)解:∵∠F=30°,∠ODF=90°,
∴∠AOD=120°,
∵OD=OB,
∵∠DOC=∠AOC=60°,
∵EB=4,∴OD=2,CD=![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目