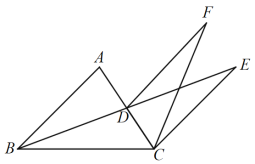
题目内容
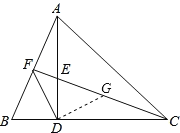
【题目】在![]() 中,
中,![]() 垂足为
垂足为![]() ,点
,点![]() 在
在![]() 上,
上,![]() 连接
连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .
.
![]() 求证:
求证:![]()
![]() 求证:
求证:![]()
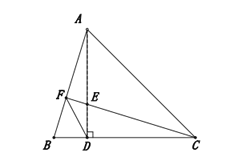
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)根据三角形高线的定义求出∠ADB=∠CDE=90°,并判断出△ACD是等腰直角三角形,根据等腰直角三角形的性质可得AD=CD,然后利用“边角边”证明△ABD和△CED全等,根据全等三角形对应角相等可得结论;
(2)在EC上截取EG=BF,根据全等三角形对应角相等可得∠B=∠CED,然后利用“边角边”证明△BDF和△EDG全等,根据全等三角形对应边相等可得DF=DG,全等三角形对应角相等可得∠BDF=∠EDG,再求出∠FDG=90°,判断出△DFG是等腰直角三角形,即可得到结论.
(1)∵AD是△ABC的高,∠ACB=45°,∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,∴AD=CD.
在△ABD和△CED中,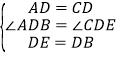 ,∴△ABD≌△CED(SAS),∴∠BAD=∠ECD;
,∴△ABD≌△CED(SAS),∴∠BAD=∠ECD;
(2)如图,在EC上截取EG=BF.
∵△ABD≌△CED,∴∠B=∠CED.在△BDF和△EDG中,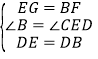 ,∴△BDF≌△EDG(SAS),∴DF=DG,∠BDF=∠EDG,∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,∴△DFG是等腰直角三角形,∴∠DFE=45°.
,∴△BDF≌△EDG(SAS),∴DF=DG,∠BDF=∠EDG,∴∠FDG=∠FDE+∠EDG=∠FDE+∠BDF=∠ADB=90°,∴△DFG是等腰直角三角形,∴∠DFE=45°.

练习册系列答案
相关题目