题目内容
【题目】如图,在平行四边形ABCD 中,边CD 5 ,对角线 AC 8 , DB 6.
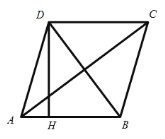
(1)求证:四边形 ABCD 是菱形;
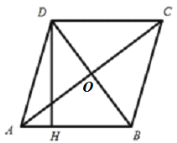
(2)过点 D 作 DH AB 于点 H ,若点 P 是线段 AC 上的一个动点,求 PH PB 的最小.
【答案】(1)见解析;(2)PH PB最小值为9.6.
【解析】
(1)根据平行四边形的性质可得OD=![]() BD,OC=
BD,OC=![]() AC,利用勾股定理的逆定理可证△OCD为直角三角形,即∠COD=90°,再根据菱形的判定定理即可得证;
AC,利用勾股定理的逆定理可证△OCD为直角三角形,即∠COD=90°,再根据菱形的判定定理即可得证;
(2)由菱形的性质可得B点关于AC的对称点是点D,则DH即为PH+PB的最小值,利用菱形的面积公式即可求得DH的长.
(1)∵四边形ABCD为平行四边形,
∴OD=![]() BD=3,OC=
BD=3,OC=![]() AC=4,
AC=4,
∵![]() ,
,
∴∠COD=90°,
∴AC与BD互相垂直平分,
∴四边形ABCD为菱形;
(2)∵BD⊥AC,OB=OD,
∴DH即为PH+PB的最小值,
∵S菱形ABCD=AC·BD=DH·AB,
∴6×8=5·DH,
解得DH=9.6.

【题目】小强在某超市同时购买A,B两种商品共三次,仅有第一次超市将A,B两种商品同时按![]() 折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
折价格出售,其余两次均按标价出售. 小强三次购买A,B商品的数量和费用如下表所示:
A商品的数量(个) | B商品的数量(个) | 购买总费用(元) | |
第一次购买 | 8 | 6 | 930 |
第二次购买 | 6 | 5 | 980 |
第三次购买 | 3 | 8 | 1040 |
(1)求 A,B商品的标价;
(2)求![]() 的值.
的值.
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和利润如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元/瓶) | 50 | 35 |
利润(元/瓶) | 20 | 15 |
(1)请求出y关于x的函数关系式;
(2)如果该厂每天至少投入成本26 400元,那么每天至少获利多少元?
(3)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?