题目内容
如图,直线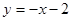 交x轴于点A,交y轴于点B,抛物线
交x轴于点A,交y轴于点B,抛物线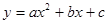 的顶点为A,且经过点B.
的顶点为A,且经过点B.
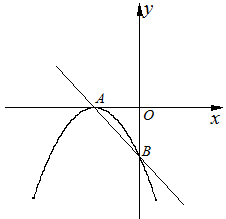
⑴求该抛物线的解析式;
⑵若点C(m,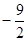 )在抛物线上,求m的值.
)在抛物线上,求m的值.
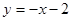 交x轴于点A,交y轴于点B,抛物线
交x轴于点A,交y轴于点B,抛物线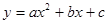 的顶点为A,且经过点B.
的顶点为A,且经过点B.
⑴求该抛物线的解析式;
⑵若点C(m,
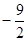 )在抛物线上,求m的值.
)在抛物线上,求m的值.解:(1)直线 .
.
令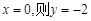 ,∴点B坐标为(0,-2).
,∴点B坐标为(0,-2).
令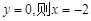 ∴点A坐标为(-2,0).
∴点A坐标为(-2,0).
设抛物线解析式为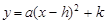 .
.
∵抛物线顶点为A,且经过点B,
∴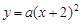 ,
,
∴-2=4a,∴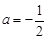 .
.
∴抛物线解析式为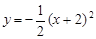 ,
,
∴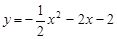 .
.
(2)方法1:
∵点C(m,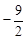 )在抛物线
)在抛物线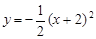 上,
上,
∴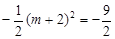 ,
,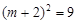 ,
,
解得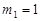 ,
,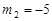 .
.
方法2:
∵点C(m,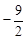 )在抛物线
)在抛物线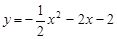 上,
上,
∴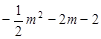
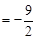 ,∴
,∴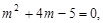
解得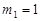 ,
,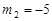 .
.
 .
.令
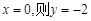 ,∴点B坐标为(0,-2).
,∴点B坐标为(0,-2).令
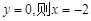 ∴点A坐标为(-2,0).
∴点A坐标为(-2,0). 设抛物线解析式为
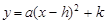 .
. ∵抛物线顶点为A,且经过点B,
∴
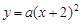 ,
,∴-2=4a,∴
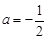 .
.∴抛物线解析式为
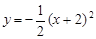 ,
,∴
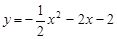 .
.(2)方法1:
∵点C(m,
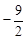 )在抛物线
)在抛物线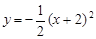 上,
上,∴
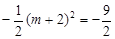 ,
,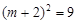 ,
,解得
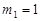 ,
,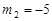 .
.方法2:
∵点C(m,
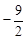 )在抛物线
)在抛物线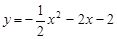 上,
上, ∴
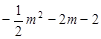
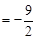 ,∴
,∴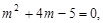
解得
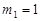 ,
,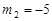 .
.(1)先根据直线解析式求出点A、点B的坐标,再根据点A为抛物线的顶点设出顶点式,再由点B的坐标根据待定系数法即可求出抛物线解析式;
(2)把点C坐标代入抛物线解析式即可得到结果。
(2)把点C坐标代入抛物线解析式即可得到结果。

练习册系列答案
相关题目

 经过点B(
经过点B( ,2),且与x轴交于点A.将抛物线
,2),且与x轴交于点A.将抛物线 沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
沿x轴作左右平移,记平移后的抛物线为C,其顶点为P.
 与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.
与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3. (
( ≠0)的对称轴是直线
≠0)的对称轴是直线 =
=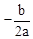

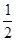 ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( ) 间,当每间客房的定价为每天
间,当每间客房的定价为每天 元时,客房会全部住满.当每间客房每天的定价每涨
元时,客房会全部住满.当每间客房每天的定价每涨 元时,就会有
元时,就会有 间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出
间客房空闲.如果旅客居住客房,宾馆需对每间客房每天支出 元的各种费用.
元的各种费用. (元)与每间客房涨价
(元)与每间客房涨价 (元)之间的函数关系式;
(元)之间的函数关系式; 元,
元, 时,下列函数中,函数值
时,下列函数中,函数值 随自变量
随自变量 增大而增大的是 (只填写序号)
增大而增大的是 (只填写序号) ;②
;② ;③
;③ ;④
;④ .
. 的最小值是 ( )
的最小值是 ( ) 2
2