题目内容
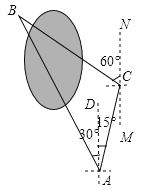
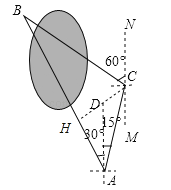
【题目】小明要测量公园北湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
【答案】(1)30°;(2)386.
【解析】
试题分析:(1)先利用平行线的性质得∠ACM=∠DAC=15°,再利用平角的定义计算出∠ACB=105°,然后根据三角形内角和计算∠ABC的度数;
(2)作CH⊥AB于H,如图,易得△ACH为等腰直角三角形,则AH=CH=![]() AC=
AC=![]() ,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=
,在Rt△BCH中利用含30度的直角三角形三边的关系得到BH=![]() CH=
CH=![]() ,AB=AH+BH=
,AB=AH+BH=![]() ,然后进行近似计算即可.
,然后进行近似计算即可.
试题解析:(1)∵CM∥AD,∴∠ACM=∠DAC=15°,∴∠ACB=180°﹣∠BCN﹣∠ACM=180°﹣60°﹣15°=105°,而∠BAC=30°+15°=45°,∴∠ABC=180°﹣45°﹣105°=30°;
(2)作CH⊥AB于H,如图,∵∠BAC=45°,∴△ACH为等腰直角三角形,∴AH=CH=![]() AC=
AC=![]() ×200=
×200=![]() ,在Rt△BCH中,∵∠HBC=30°,∴BH=
,在Rt△BCH中,∵∠HBC=30°,∴BH=![]() CH=
CH=![]() ,∴AB=AH+BH=
,∴AB=AH+BH=![]() ≈141.4+244.9≈386.
≈141.4+244.9≈386.
答:两棵大树A和B之间的距离约为386米.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】在我县中学生春季田径运动会上,参加男子跳高的16名运动员的成绩如下表所示:
成绩(m) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
人数 | 1 | 3 | 3 | 4 | 3 | 2 |
这些运动员跳高成绩的中位数和众数分别是( )
A.1.70,1.65
B.1.70,1.70
C.1.65,1.70
D.3,3