题目内容
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.
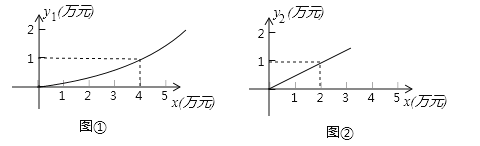
(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
【答案】(1)![]() ,
,![]() ;(2)苗圃至少获得4万元利润,最多能获得8万元利润.
;(2)苗圃至少获得4万元利润,最多能获得8万元利润.
【解析】
试题分析:(1)利用待定系数法求两个函数的解析式;
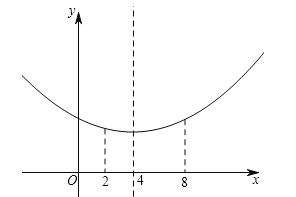
(2)根据总投资成本为10万元,设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10﹣x)万元,列函数关系式,发现是二次函数,画出函数图象,找出当2≤x≤8时的最小利润和最大利润.
试题解析:(1)把(4,1)代入![]() 中得:
中得:
16a=1,a=![]() ,∴
,∴![]() .
.
把(2,1)代入![]() =kx中得:
=kx中得:
2k=1,k=![]() ,∴
,∴![]() ;
;
(2)设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10﹣x)万元,则W=![]() =
=![]() =
=![]() ,由图象得:当2≤x≤8时,当x=4时,W有最小值,W小=4,当x=8时,W有最大值,W大=
,由图象得:当2≤x≤8时,当x=4时,W有最小值,W小=4,当x=8时,W有最大值,W大=![]() (8﹣4)2+4=5.
(8﹣4)2+4=5.
答:苗圃至少获得4万元利润,最多能获得8万元利润.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目