题目内容
【题目】在正方形ABCD中,以CD为底边在正方形外侧作等腰△CDE,连接BE与对角线AC交于点P、与CD交于点H,连接PD.
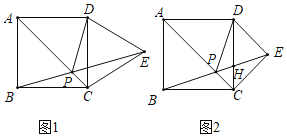
(1)如图1,当∠DEC=60°时,求证:PA=PE;
(2)如图2,当∠DEC=90°时,
①求tan∠EBC的值;②求![]() 的值.
的值.
【答案】(1)见解析;(2)①tan∠EBC=![]() ;②
;②![]() .
.
【解析】
(1)通过计算证明∠ADP=∠EDP=75°,证明△ADP≌△EDP即可.
(2)①如图2﹣1中,过点E作EF⊥BC的延长线于F,设CF=a.想办法求出EF,BF即可解决问题.
②方法一:如图2﹣1中延长DP交BC于点Q,先推证P为BE的中点,得PE=![]() ,利用相似三角形的性质解决问题即可.
,利用相似三角形的性质解决问题即可.
方法二:如图2﹣2中,作EG⊥CD于G,设GH=x,利用相似三角形的性质求解即可.
(1)证明:如图1中,

∵四边形ABCD是正方形.
∴AB=AD,∠BAP=∠DAP,
∵AP=AP,
∴△ABP≌△ADP(SAS)
∴∠APD=∠APB.
∵CB=CE,
∴∠CBE=∠CEB.
∵∠BCE=∠BCD+∠DCE=90°+60°=150°,
∴∠CBE=15°.
∵∠ACB=45°,
∴∠APB=∠ACB+∠CBE=60°.
∴∠APD=60°,
∴ADP=180°﹣45°﹣60°=75°,
∵∠ADE=90°+60°=150°,
∴∠ADP=∠EDP=75°,
∵DA=DE,DP=DP,
∴△ADP≌△EDP(SAS),
∴PA=PE.
(2)①如图2﹣1中,过点E作EF⊥BC的延长线于F,设CF=a.
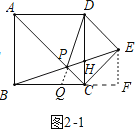
∵ED=EC,∠DEC=90°,
∴∠DCE=45°,
∵∠DCF=∠EFC=90°,
∴∠ECF=∠CEF=45°,
∴EF=CF=a,EC=![]() a,BC=CD=2a,
a,BC=CD=2a,
∴BF=3a,
在Rt△BEF中,tan∠EBC=![]() .
.
②方法一:如图2﹣1中延长DP交BC于点Q,先推证P为BE的中点,得PE=![]() ,
,
由![]() 得CH=
得CH=![]() ,又CH=CQ,
,又CH=CQ,
∴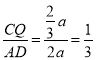
由△CQP∽△APD得![]() ,
,
∴PA=![]() ,
,
∴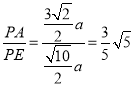 .
.
方法二:如图2﹣2中,作EG⊥CD于G,设GH=x,
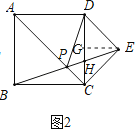
由GE‖BC得△EGH∽△BCH,得CH=2GH=2x,
∴BC=3CH=6x
由PC‖DE得△PCH∽△EDH,得![]() ,
,
又DE=CG=3x,DE=3![]() x,
x,
∴PC=![]()
又AC=6![]() x,
x,
∴PA=![]() ,PE=
,PE=![]() ,
,
则![]() .
.

【题目】今年5月份,十八中九年级学生参加了中考体育模拟考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表和扇形统计图,根据图表中的信息解答下列问题:
分组 | 分数段(分)) | 频数 |
A | 26≤x<31 | 2 |
B | 31≤x<36 | 5 |
C | 36≤x<41 | 15 |
D | 41≤x<46 | m |
E | 46≤x<51 | 10 |
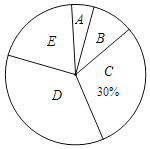
(1)求全班学生人数和m的值.
(2)求扇形统计图中的E对应的扇形圆心角的度数;
(3)该班中考体育成绩满分共有3人,其中男生2人,女生1人,现需从这3人中随机选取2人到八年级进行经验交流,请用“列表法”或“画树状图法”求出恰好选到一男一女的概率.