题目内容
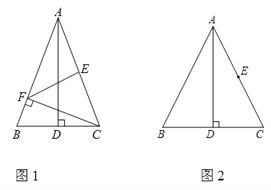
【题目】如图,∠CAB=∠ABD=50°,P为AB中点,点M为射线AC上(不与点A重合)的任意一点,连接MP,并使MP的延长线交射线BD于点N,设∠BPN=α.连接MB,NA.
(1)求证:四边形MBNA为平行四边形;
(2)当α=____°时,四边形MBNA为矩形;
(3)当α=_____°时,四边形MBNA为菱形;
(4)四边形MBNA可能是正方形吗?_____(回答“可能”或“不可能”)

【答案】(1)证明见解析;(2)80;(3)90;(4)不可能.
【解析】
(1)由“AAS”可证△APM≌△BPN,可得AM=BN,即可得结论;
(2)由矩形的性质和三角形的内角和定理可求解;
(3)由菱形的性质可求解;
(4)由正方形的性质可求解.
(1) 证明:∵P为AB中点,
∴AP=BP
∵∠CAB=∠ABD=50°,
∴AM∥BN
∴∠AMP=∠BNP,且AP=BP,∠CAB=∠ABD=50°,
∴△APM≌△BPN(AAS)
∴AM=BN,且AM∥BN
∴四边形MBNA为平行四边形;
(2)若四边形MBNA为矩形
∴BP=AP=MP=NP
∴∠ABN=∠MNB=50°
∴α=180°﹣50°﹣50°=80°
故答案为:80
(3)若四边形MBNA为菱形
∴AB⊥MN
∴α=90°
故答案为:90
(4)若四边形MBNA为正方形
∴∠ABD=45°≠50°
∴四边形MBNA不可能为正方形
故答案为:不可能

 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
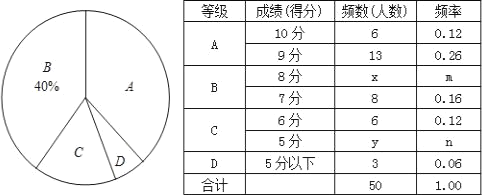
活力试卷系列答案【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
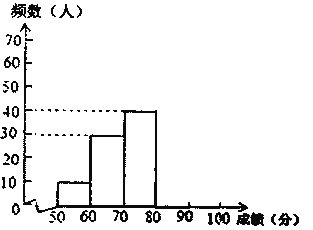
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?
【题目】某新建小区要修一条1050米长的路,甲、乙两个工程队想承建这项工程.经
了解得到以下信息(如表):
工程队 | 每天修路的长度(米) | 单独完成所需天数(天) | 每天所需费用(元) |
甲队 | 30 | n | 600 |
乙队 | m | n﹣14 | 1160 |
(1)甲队单独完成这项工程所需天数n= ,乙队每天修路的长度m= (米);
(2)甲队先修了x米之后,甲、乙两队一起修路,又用了y天完成这项工程(其中x,y为正整数).
①当x=90时,求出乙队修路的天数;
②求y与x之间的函数关系式(不用写出x的取值范围);
③若总费用不超过22800元,求甲队至少先修了多少米.