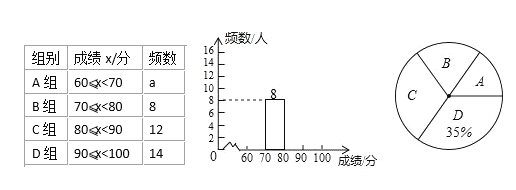
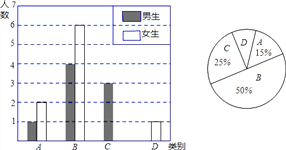
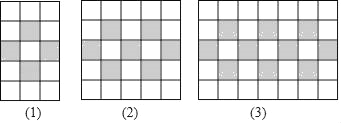
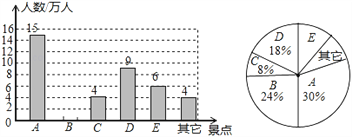
题目内容
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=![]() ,△BOC≌△ADC,∠OCD=60°,连接OD.
,△BOC≌△ADC,∠OCD=60°,连接OD.
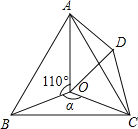
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试求证:△AOD是直角三角形;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
【答案】(1)见解析;
(2)△AOD是Rt△.理由见解析;
(3)不能.理由:见解析;
(4)当α=110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据全等三角形的性质得到OC=DC,根据等边三角形的判定定理证明即可;
(2)根据全等三角形的性质得到∠ADC=∠BOC=∠α=150°,结合图形计算即可;
(3)用反证法,假设△AOD能否为等边三角形,根据题意证明∠AOC+∠AOB+∠BOC不等于360°,推出矛盾;
(4)分∠AOD=∠ADO、∠AOD=∠OAD、∠ADO=∠OAD三种情况,根据等腰三角形的判定定理计算即可.
(1)证明:∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形;
(2)△AOD是Rt△.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC∠ODC=150°60°=90°,
∴△AOD是Rt△;
(3)不能.理由:
由△BOC≌△ADC,得∠ADC=∠BOC=∠α.
若△AOD为等边三角形,
则∠ADO=60°,
又∵∠ODC=60°,
∴∠ADC=∠α=120°.
又∵∠AOD=∠DOC=60°,
∴∠AOC=120°,
又∵∠AOB=110°,
∴∠AOC+∠AOB+∠BOC=120°+120°+110°=350°<360°.
∴△AOD不可能为等边三角形;
(4)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°∠AOB∠BOC∠COD=360°110°α60°=190°α,
∠ADO=∠ADC∠ODC=α60°,
∴∠OAD=180°∠AOD∠ADO=180°(190°α)(α60°)=50°.
①当∠AOD=∠ADO时,190°α=α60°,∴α=125°.
②当∠AOD=∠OAD时,190°α=50°,∴α=140°.
③当∠ADO=∠OAD时,α60°=50°,∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.

 名校课堂系列答案
名校课堂系列答案【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.