题目内容
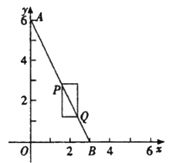
【题目】如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.
(1)点B的坐标为(3,0);
①若点P的横坐标为![]() ,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是 .
(2)四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;
①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围 .
【答案】(1)①9,②(1,2);(2)①(1,5)或(5,1),②![]()
【解析】
(1)①根据题意求出PE,EQ即可解决问题.
②求出点P、Q的“涵矩形”的长与宽即可判断.
(2)①求出正方形的边长,分两种情形分别求解即可解决问题.
②点M在直线y=-x+5上运动,设直线y=-x+5交x轴于F,交y轴于E,作OD⊥EF于D.求出OM的最大值,最小值即可判断.
解:(1)①如图1中,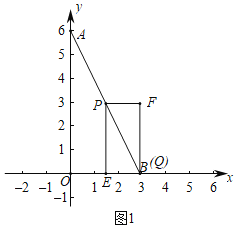
由题意:矩形PEQF中,EQ=PF=3-![]() ,
,
∴OE=EQ,
∵EP∥OA,
∴AP=PQ,
∴PE=QF=![]() OA=3,
OA=3,
∴点P、Q的“涵矩形”的周长=(3+![]() )×2=9.
)×2=9.
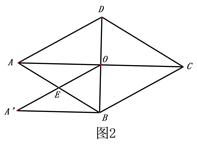
②如图2中,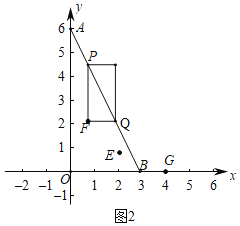
∵点P、Q的“涵矩形”的周长为6,
∴邻边之和为3,
∵矩形的长是宽的两倍,
∴点P、Q的“涵矩形”的长为2,宽为1,
∵P(1,4),F(1,2),
∴PF=2,满足条件,
∴F(1,2)是矩形的顶点.
(2)①如图3中,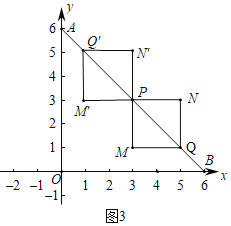
∵点P、Q的“涵矩形”是正方形,
∴∠ABO=45°,
∴点A的坐标为(0,6),
∴点B的坐标为(6,0),
∴直线AB的函数表达式为y=-x+6,
∵点P的横坐标为3,
∴点P的坐标为(3,3),
∵正方形PMQN的周长为8,
∴点Q的横坐标为3-2=1或3+2=5,
∴点Q的坐标为(1,5)或(5,1).
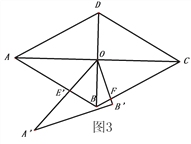
②如图4中,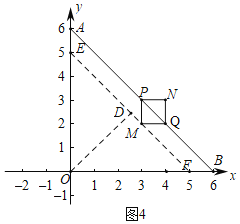
∵正方形PMQN的对角线为![]() ,
,
∴PM=MQ=1,
易知M在直线y=-x+5上运动,设直线y=-x+5交x轴于F,交y轴于E,作OD⊥EF于D,
∵OE=OF=5,
∴EF=![]() ,
,
∵OD⊥EF,
∴ED=DF,
∴OD=![]() EF=
EF=![]() ,
,
∴OM的最大值为5,最小值为![]() ,
,
∴![]() .
.

 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案