题目内容
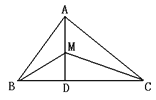
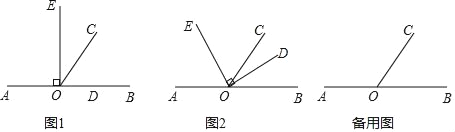
【题目】如图所示,在直线AB上的一点O,以O为端点依次作射线OE,OC,OD,使∠EOD=90°,∠COB=60°
(1)如图1当∠EOD的一边OD在射线OB上时,求∠COE的度数;
(2)如图2当∠EOD绕着点O逆时针旋转到OC平分∠BOE时,求∠COD的度数;
(3)当∠EOD绕着点O逆时针旋转,且O°<∠AOE<90°(但≠60°)时,试猜想∠AOE与∠COD有怎样的数量关系,并说明理由.
【答案】(1)30;(2)30°;(3)当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°;
【解析】
(1)根据∠COE=∠EOB-∠BOC计算即可;
(2)根据∠COD=∠EOD-∠EOC,只要求出∠EOC即可;
(3)当60°<∠AOE<90°时,∠AOE-∠COD=30°;当0<∠AOE<60°时,∠AOE+∠COD=30°.
(1)∵∠COE=∠EOB﹣∠BOC,∠EOD=90°,∠COB=60°
∴∠COE=90°﹣60°=30°,
(2)∵OC 平分∠BOE,
∴∠BOC=∠COE=60°,
∴∠COD=∠EOD﹣∠EOC=90°﹣60°=30°;
(3)①如图2中,当60°<∠AOE<90°时,
∵∠EOD=90°,
∴∠AOE+∠DOB=90°,
∴∠AOE+(60°﹣∠COD)=90°,
∴∠AOE﹣∠COD=30°
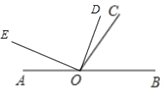
②如图3中,当0<∠AOE<60°时,∵∠AOC=180°﹣∠BOC=120°,∠EOD=90°,
∴∠AOE+∠COD=30°;
综上所述,当60°<∠AOE<90°时,∠AOE﹣∠COD=30°;
当0<∠AOE<60°时,∠AOE+∠COD=30°.

【题目】甲、乙两组各有12名学生,组长绘制了本组5月份家庭用水量的统计图表,如图, 甲组12户家庭用水量统计表
用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 4 | 5 | 2 | 1 |
比较5月份两组家庭用水量的中位数,下列说法正确的是( )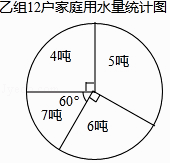
A.甲组比乙组大
B.甲、乙两组相同
C.乙组比甲组大
D.无法判断