Question

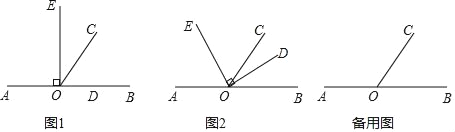
【题目】如图，四边形ABCD是正方形，点E是平面内异于点A的任意一点，以线

段AE为边作正方形AEFG，连接EB，GD．

(1) 如图1，判断EB与GD的关系并说明理由；

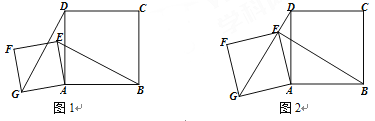
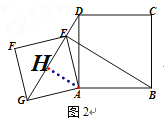
(2) 如图2，若点E在线段DG上，AB＝5，AG＝3，求BE的长．

Answer 1

【答案】(1)EB=GD,EB⊥GD,；(2)BE=7

【解析】分析:（1）由正方形的性质得AG=AE,AB=AD, ∠EAG=∠BAD=90°，从而根据“SSA”证明△ADG和△ABE即可得到结论；

（2）作AH⊥GF于点H.在Rt△AGE中求出GE、AH、GH的值，在Rt△AHD中求出DH的值，从而可求出GD和BE的值.

详解:（1）∵四边形ABCD和四边形AEFG是正方形，

∴AG=AE,AB=AD, ∠EAG=∠BAD=90°,

∴∠DAG=∠BAE.

在△ADG和△ABE中，

∵AG=AE,

∠DAG=∠BAE,

AB=AD,

∴△ADG≌△ABE，

∴EB=GD;

（2）作AH⊥GF于点H.

∵AG=AE＝3,

∴GE=,

∴AH=GH=,

∴DH=,

∴BE=GD=DH+CH=4+3=7.