题目内容
【题目】（本题满分8分）一列快车由甲地开往乙地，一列慢车由乙地开往甲地，两车同时出发，匀速
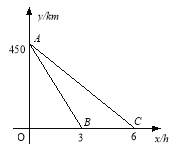
运动．快车离乙地的路程y1 （km）与行驶的时间x（h）之间的函数关系，如图中线段AB所示．慢车离甲地的路
程y2（km）与行驶的时间x（h）之间的函数关系，如图中线段AC所示．根据图像进行以下研究．
解读信息：（1）甲、乙两地之间的距离为 km；
（2）线段AB的解析式为 ； 两车在慢车出发 小时后相遇；
问题解决：
（3）设快、慢车之间的距离为y（km），求y与慢车行驶时间x（h）的函数关系式，并画出函数的图像．
【答案】（1）甲、乙两地之间的距离为 450 km;
（2）线段AB的解析式为 y1＝450－150 x （0≤x≤3）； 两车在慢车出发 2 小时后相遇；
（3）
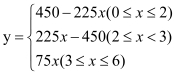
其图象为折线图
拐点处的数据一定要标出，若未标出，扣分。
【解析】
试题（1）根据图像中点A的坐标可知甲、乙两地之间的距离为 450km；（2）线段AB的解析式为y=kx+b把点A（0，450），B（3，0）代入y=kx+b，然后解方程组即可，根据图象可求出快车的速度
千米/小时，是慢车的速度是
千米/小时，所以两车在慢车出发
小时后相遇；（3）分三种情况讨论：
即可．
试题解析：（1）根据图像中点A的坐标可知甲、乙两地之间的距离为 450km；（2）线段AB的解析式为y=kx+b把点A（0，450），B（3，0）代入y=kx+b得
解得
，所以y1＝450－150 x （0≤x≤3），根据图象可求出快车的速度千米/小时，是慢车的速度是千米/小时，所以两车在慢车出发小时后相遇；（3）分三种情况讨论：当
时，y=450-225x，当
时，y=225x-450，当
时，y=75x，所以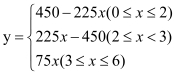，其图象为折线图
练习册系列答案
课程达标测试卷闯关100分系列答案
新卷王期末冲刺100分系列答案
全能闯关100分系列答案
相关题目
