题目内容
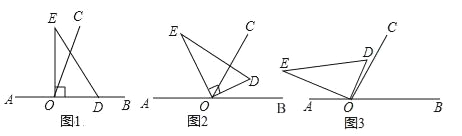
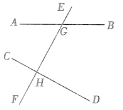
【题目】如图,直线AB,CD被直线EF所截,交点分别为G,H, ∠CHG=∠DHG=![]() ∠AGE.
∠AGE.
(1)CD与EF有怎样的位置关系?请说明理由.
(2)求∠CHG的同位角、内错角、同旁内角的度数.
【答案】(1)CD⊥EF;(2) ∠CHG的同位角∠AGE=120°,内错角∠BGF=∠AGE=120°,同旁内角∠AGF=60°
【解析】
(1)先由∠CHG+∠DHG=180°及∠CHG=∠DHG,可得∠CHG=∠DHG =90°,再根据垂直的定义得到CD与EF互相垂直;
(2)先由∠CHG=∠DHG =![]() ∠AGE,可得∠AGE=120°,再根据同位角、内错角、同旁内角的定义即可求解.
∠AGE,可得∠AGE=120°,再根据同位角、内错角、同旁内角的定义即可求解.
(1)CD⊥EF.理由如下:
因为CD是直线,所以∠CHG+∠DHG=180°,
又∠CHG=∠DHG,所以∠CHG=∠DHG=90°,
所以CD⊥EF.
(2)由(1)知∠CHG=∠DHG=90°,
因为∠CHG=∠DHG=![]() ∠AGE,
∠AGE,
所以∠AGE=120°,
所以∠CHG的同位角∠AGE=120°,内错角∠BGF=∠AGE=120°,同旁内角∠AGF=180°-∠AGE=60°.

练习册系列答案
相关题目