题目内容
(2013•台州)如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”.
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA=
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB-BC和AD-DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题,作对另加2分,但全卷满分不超过150分)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)
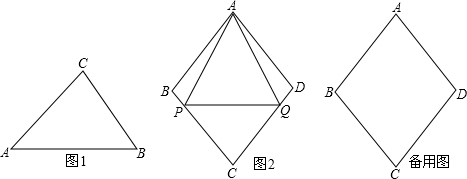
(1)请用直尺和圆规画一个“好玩三角形”;
(2)如图在Rt△ABC中,∠C=90°,tanA=
| ||
| 2 |
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同速度分别沿折线AB-BC和AD-DC向终点C运动,记点P经过的路程为s.
①当β=45°时,若△APQ是“好玩三角形”,试求
| a |
| s |
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”.请直接写出tanβ的取值范围.
(4)(本小题为选做题,作对另加2分,但全卷满分不超过150分)
依据(3)的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是‘好玩三角形’的个数关系”的真命题(“好玩三角形”的个数限定不能为1)

分析:(1)先画一条线段AB,再确定AB的中点O,以点O为圆心,AB为半径画圆,在圆O上取一点C,连接AC、BC,则△ABC是所求作的三角形;
(2)取AC的中点D,连接BD,设BC=
x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BD,从而得出结论;
(3)①当β=45°时,分情况讨论,P点在AB上时,△APQ是等腰直角三角形,不可能是“好玩三角形”,当P在BC上时,延长AB交QP的延长线于点F,可以求出分情况讨论,就可以求出
=
,再分情况讨论就可以求出当AE=PQ时,
的值,当AP=QM时,可以求出
的值;
②根据①求出的两个
的值就可以求出tanβ的取值范围;
(4)由(3)可以得出0<tanβ<
,△APQ为“好玩三角形”的个数为2就是真命题.
(2)取AC的中点D,连接BD,设BC=
| 3 |
(3)①当β=45°时,分情况讨论,P点在AB上时,△APQ是等腰直角三角形,不可能是“好玩三角形”,当P在BC上时,延长AB交QP的延长线于点F,可以求出分情况讨论,就可以求出
| AE |
| PE |
| s |
| 2a-s |
| a |
| s |
| a |
| s |
②根据①求出的两个
| AE |
| PE |
(4)由(3)可以得出0<tanβ<
| ||
| 3 |
解答: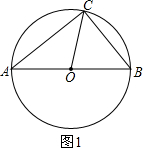 解:(1)如图1,①作一条线段AB,
解:(1)如图1,①作一条线段AB,
②作线段AB的中点O,
③以点O为圆心,AB为半径画圆,
④在圆O上取一点C,连接AC、BC,
∴△ABC是所求作的三角形.
(2)如图2,取AC的中点D,连接BD
∵∠C=90°,tanA=
,
∴
=
∴设BC=
x,则AC=2x,
∵D是AC的中点,
∴CD=
AC=x
∴BD=
=
=2x,
∴AC=BD
∴△ABC是“好玩三角形”;
(3)①如图3,当β=45°,点P在AB上时,
∴∠ABC=2β=90°,
∴△APQ是等腰直角三角形,不可能是“好玩三角形”,
当P在BC上时,连接AC交PQ于点E,延长AB交QP的延长线于点F,
∵PC=CQ,
∴∠CAB=∠ACP,∠AEF=∠CEP,
∴△AEF∽△CEP,
∴
=
=
=
.
∵PE=CE,
∴
=
.
Ⅰ当底边PQ与它的中线AE相等时,即AE=PQ时,
=
=2,
∴
=
,
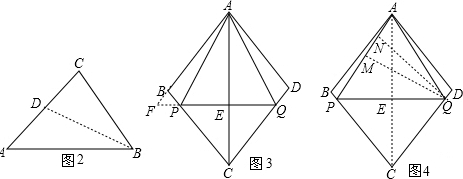
Ⅱ当腰AP与它的中线QM相等,即AP=QM时,
作QN⊥AP于N,如图4
∴MN=AN=
MP.
∴QN=
MN,
∴tan∠APQ=
=
=
,
∴tan∠APE=
=
=
,
∴
=
+
②由①可知,当AE=PQ和AP=QM时,有且只有一个△APQ能成为“好玩三角形”,
∴
<tanβ<2时,有且只有一个△APQ能成为“好玩三角形”.
(4)由(3)可以知道0<tanβ<
,
则在P、Q的运动过程中,使得△APQ成为“好玩三角形”的个数为2.
 解:(1)如图1,①作一条线段AB,
解:(1)如图1,①作一条线段AB,②作线段AB的中点O,
③以点O为圆心,AB为半径画圆,
④在圆O上取一点C,连接AC、BC,
∴△ABC是所求作的三角形.
(2)如图2,取AC的中点D,连接BD
∵∠C=90°,tanA=
| ||
| 2 |
∴
| BC |
| AC |
| ||
| 2 |
∴设BC=
| 3 |
∵D是AC的中点,
∴CD=
| 1 |
| 2 |
∴BD=
| CD2+BC2 |
| 3x2+x2 |
∴AC=BD
∴△ABC是“好玩三角形”;
(3)①如图3,当β=45°,点P在AB上时,
∴∠ABC=2β=90°,
∴△APQ是等腰直角三角形,不可能是“好玩三角形”,
当P在BC上时,连接AC交PQ于点E,延长AB交QP的延长线于点F,
∵PC=CQ,
∴∠CAB=∠ACP,∠AEF=∠CEP,
∴△AEF∽△CEP,
∴
| AE |
| CE |
| AF |
| PC |
| AB+BP |
| PC |
| s |
| 2a-s |

∵PE=CE,
∴
| AE |
| PE |
| s |
| 2a-s |
Ⅰ当底边PQ与它的中线AE相等时,即AE=PQ时,
| AE |
| PE |
| s |
| 2a-s |
∴
| a |
| s |
| 3 |
| 4 |
Ⅱ当腰AP与它的中线QM相等,即AP=QM时,
作QN⊥AP于N,如图4
∴MN=AN=
| 1 |
| 2 |
∴QN=
| 15 |
∴tan∠APQ=
| QN |
| PN |
| ||
| 3MN |
| ||
| 3 |
∴tan∠APE=
| AE |
| PE |
| s |
| 2a-s |
| ||
| 3 |
∴
| a |
| s |
| ||
| 10 |
| 1 |
| 2 |
②由①可知,当AE=PQ和AP=QM时,有且只有一个△APQ能成为“好玩三角形”,
∴
| ||
| 3 |
(4)由(3)可以知道0<tanβ<
| ||
| 3 |
则在P、Q的运动过程中,使得△APQ成为“好玩三角形”的个数为2.
点评:本题是一道相似形综合运用的试题,考查了相似三角形的判定及性质的运用,勾股定理的运用,等腰直角三角形的性质的运用,等腰三角形的性质的运用,锐角三角形函数值的运用,解答时灵活运用三角函数值建立方程求解是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•台州)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )
(2013•台州)如图,已知边长为2的正三角形ABC顶点A的坐标为(0,6),BC的中点D在y轴上,且在点A下方,点E是边长为2、中心在原点的正六边形的一个顶点,把这个正六边形绕中心旋转一周,在此过程中DE的最小值为( )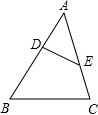 (2013•台州)如图,在△ABC中,点D,E分别在边AB,AC上,且
(2013•台州)如图,在△ABC中,点D,E分别在边AB,AC上,且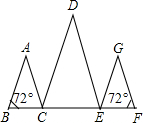 (2013•台州)如图,点B,C,E,F在一直线上,AB∥DC,DE∥GF,∠B=∠F=72°,则∠D=
(2013•台州)如图,点B,C,E,F在一直线上,AB∥DC,DE∥GF,∠B=∠F=72°,则∠D=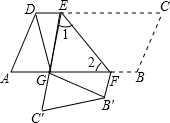 (2013•台州)如图,在?ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.
(2013•台州)如图,在?ABCD中,点E,F分别在边DC,AB上,DE=BF,把平行四边形沿直线EF折叠,使得点B,C分别落在B′,C′处,线段EC′与线段AF交于点G,连接DG,B′G.