题目内容
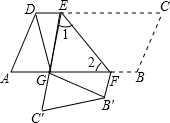（2013•台州）如图，在?ABCD中，点E，F分别在边DC，AB上，DE=BF，把平行四边形沿直线EF折叠，使得点B，C分别落在B′，C′处，线段EC′与线段AF交于点G，连接DG，B′G．求证：（1）∠1=∠2；
（2）DG=B′G．
分析：（1）根据平行四边形得出DC∥AB，推出∠2=∠FEC，由折叠得出∠1=∠FEC=∠2，即可得出答案；
（2）求出EG=B′G，推出∠DEG=∠EGF，由折叠求出∠B′FG=∠EGF，求出DE=B′F，证△DEG≌△B′FG即可．
（2）求出EG=B′G，推出∠DEG=∠EGF，由折叠求出∠B′FG=∠EGF，求出DE=B′F，证△DEG≌△B′FG即可．
解答：证明：（1）∵在平行四边形ABCD中，DC∥AB，
∴∠2=∠FEC，
由折叠得：∠1=∠FEC，
∴∠1=∠2；
（2）∵∠1=∠2，
∴EG=GF，
∵AB∥DC，
∴∠DEG=∠EGF，
由折叠得：EC′∥B′F，
∴∠B′FG=∠EGF，
∵DE=BF=B′F，
∴DE=B′F，
∴△DEG≌△B′FG（SAS），
∴DG=B′G．
∴∠2=∠FEC，
由折叠得：∠1=∠FEC，
∴∠1=∠2；
（2）∵∠1=∠2，
∴EG=GF，
∵AB∥DC，
∴∠DEG=∠EGF，
由折叠得：EC′∥B′F，
∴∠B′FG=∠EGF，
∵DE=BF=B′F，
∴DE=B′F，
∴△DEG≌△B′FG（SAS），
∴DG=B′G．
点评：本题考查了平行四边形性质，折叠性质，平行线性质，全等三角形的性质和判定的应用，主要考查学生的推理能力．
练习册系列答案
相关题目
（2013•台州）如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）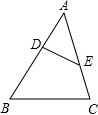
（2013•台州）如图，在△ABC中，点D，E分别在边AB，AC上，且
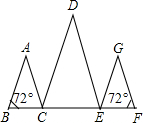（2013•台州）如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=