题目内容
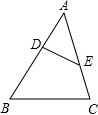（2013•台州）如图，在△ABC中，点D，E分别在边AB，AC上，且| AE |
| AB |
| AD |
| AC |
| 1 |
| 2 |
分析：首先根据两边对应成比例且夹角相等的两三角形相似，证得△ADE∽△ACB，再由相似三角形面积的比等于相似比的平方即可求得答案．
解答：解：在△ADE与△ACB中，
，
∴△ADE∽△ACB，
∴S△ADE：S△ACB=（AE：AB）2=1：4，
∴S△ADE：S四边形BCED=1：3．
故选C．
|
∴△ADE∽△ACB，
∴S△ADE：S△ACB=（AE：AB）2=1：4，
∴S△ADE：S四边形BCED=1：3．
故选C．
点评：此题考查了相似三角形的判定与性质．注意相似三角形的面积的比等于相似比的平方．
练习册系列答案
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
相关题目
（2013•台州）如图，已知边长为2的正三角形ABC顶点A的坐标为（0，6），BC的中点D在y轴上，且在点A下方，点E是边长为2、中心在原点的正六边形的一个顶点，把这个正六边形绕中心旋转一周，在此过程中DE的最小值为（ ）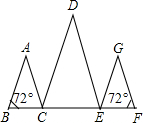
（2013•台州）如图，点B，C，E，F在一直线上，AB∥DC，DE∥GF，∠B=∠F=72°，则∠D=
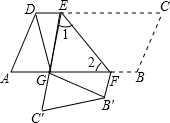（2013•台州）如图，在?ABCD中，点E，F分别在边DC，AB上，DE=BF，把平行四边形沿直线EF折叠，使得点B，C分别落在B′，C′处，线段EC′与线段AF交于点G，连接DG，B′G．