��Ŀ����
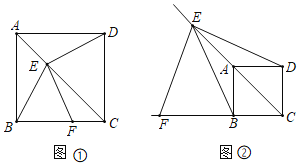
����Ŀ����ͼ�����ó�����ͬ��Сľ����һ�����ɴ�ɵ�ͼ�Σ�ͼ����5��Сľ������һ������Σ�ͼ����9��Сľ��������������Σ�ͼ����13��Сľ��������������Σ�����

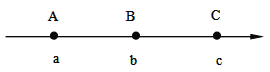
��1�����˹��ɴ���ȥ�����n��ͼ������ ��Сľ������ֱ��д�������
��2���Ƿ����ij��ͼǡ������2 019��Сľ����������ڣ������ǵڼ���ͼ�Σ���������ڣ�������2019��Сľ����ͼʾ��������ܴ���ٸ�����Σ���ʣ����ٸ�Сľ����
���𰸡���1��4n+1��2�������ڣ�����ܴ�504������Σ���ʣ2��ľ��
��������
��1�����ݹ۲�õ���ÿ����һ������Σ�������4���ߣ����ݸù����ҵ�ͨ�ʽ��ʽ.
��2���1���õ��ĵ�ͨ�ʽ����2019��ȥ��⣬���Ϊ������ǡ�ô��ڣ���Ϊ����ʱ���������������.
��1�����ݹ۲�õ���ÿ����һ������Σ�������4���ߣ���һ��ͼ��5���ߣ��ڶ���ͼ��5+4=9���ߣ�������ͼ��5+4+4=5+4��2=13���ߣ����ĸ�ͼ��5+4+4+4=5+4��3=17���ߣ����մ˹������n��ͼ����5+��n-1����4=4n+1����.
���n��ͼ������4n+1��ľ��.
��2����4n+1=2019����4n=2018����ʱn=504��2����ֻ�ܰڳ�504������Σ�504���������Ҫ4��504+1=2017��ľ����2019-2017=2����ʣ2��ľ��.

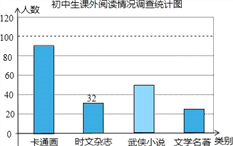
����Ŀ��ijУ��������˲���ѧ������������ϲ����ͼ���������ֻѡһ���ѧ�������Ķ���������˵���ͳ�ƣ���������ͳ�ƺ���Ƴ�����ͳ�Ʊ�������ͳ��ͼ�������ͳ��ͼ���ṩ����Ϣ����������⣺
���� | Ƶ�� | Ƶ�� |
��ͨ�� | a | 0.45 |
ʱ����־ | b | 0.16 |
����С˵ | 50 | c |
��ѧ���� | d | e |
��1���������������� ����ѧ����ͳ�Ʊ���d=�� ����
��2�������Դ�ͳ�Ʊ��������ͳ��ͼ��������С˵��Ӧ��Բ�Ľ����� ����
��3���Թ��Ƹ�У1500��ѧ�����ж�����ͬѧ��ϲ����ѧ�������鼮��