题目内容
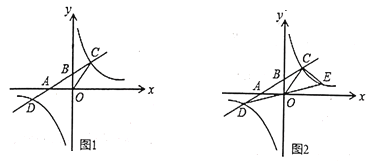
【题目】如图,直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+
分别与x轴、y轴交于B,C两点,点A在x轴上,∠ACB=90°,抛物线y=ax2+bx+![]() 经过A,B两点,A点坐标为(﹣1,0).
经过A,B两点,A点坐标为(﹣1,0).
(1)求B、C两点的坐标;
(2)求抛物线的解析式;
(3)点M是直线BC上方抛物线上的一点,过点M作MH⊥BC于点H,作MD∥y轴交BC于点D,求△DMH周长的最大值.

【答案】(1)B(3,0),C(0, ![]() );(2)y=﹣
);(2)y=﹣![]() x2+
x2+![]() x+
x+![]() ;(3)
;(3)![]()
【解析】试题分析:(1)分别令x,y得零,求坐标.(2)利用待定系数法求二次函数解析式.(3)建立△DMH二次函数关系,求最值即可.
试题解析:
(1)∵直线y=﹣![]() x+
x+![]() 分别与x轴、y轴交于B、C两点,
分别与x轴、y轴交于B、C两点,
∴B(3,0),C(0, ![]() );
);
(2)∵抛物线y=ax2+bx+![]() 经过A,B两点,
经过A,B两点,
∴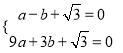 ,
,
解得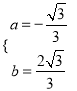 .
.
∴抛物线解析式为y=﹣![]() x2+
x2+![]() x+
x+![]()
(3)∵B(3,0),C(0, ![]() );
);
∴OB=3,OC=![]() ,
,
∴tan∠BCO=![]() ,
,
∴∠BCO=60°,
∵MD∥y轴,MH⊥BC,
∴∠MDH=∠BCO=60°,则∠DMH=30°,
∴DH=![]() DM,MH=
DM,MH=![]() DM,
DM,
∴△DMH的周长=DM+DH+MH=DM+![]() DM+
DM+![]() DM=
DM=![]() DM,
DM,
∴当DM有最大值时,其周长有最大值,
∵点M是直线BC上方抛物线上的一点,
∴可设M(t,﹣ ![]() t2+
t2+![]() t+
t+![]() ),则D(t,﹣
),则D(t,﹣![]() t+
t+![]() ),
),
∴DM=﹣![]() t2+
t2+![]() t+
t+![]() ﹣(﹣
﹣(﹣![]() t+
t+![]() )=﹣
)=﹣![]() (t﹣
(t﹣![]() )2+
)2+![]() ,
,
∴当t=![]() 时,DM有最大值,最大值为
时,DM有最大值,最大值为![]() ,
,
此时![]() DM=
DM=![]() ,
,
即△DMH周长的最大值为![]() .
.

 考前必练系列答案
考前必练系列答案【题目】佳乐家超市元旦期间搞促销活动,活动方案如下表:
一次性购物 | 优惠方案 |
不超过200元 | 不给予优惠 |
超过200元,而不超过1000元 | 优惠10% |
超过1000元 | 其中1000元按8.5折优惠,超过部分按7折优惠 |
小颖在促销活动期间两次购物分别支付了134元和913元.
(1)小颖两次购买的物品如果不打折,应支付多少钱?
(2)在此活动中,他节省了多少钱?