题目内容
【题目】如图,已知直线![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() .
.
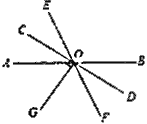
(1)求![]() 的度数.
的度数.
(2)![]() 是
是![]() 的平分线吗?说明你的理由.
的平分线吗?说明你的理由.
【答案】(1)∠AOG=54°;(2)OC是∠AOE的角平分线;理由见解析.
【解析】
(1)由对顶角相等可得∠AOC的度数,由OG⊥CD可得∠COG=∠DOG=90°,利用角的和差关系即可求出∠AOG的度数;
(2)根据角平分线的定义可得∠AOG=∠FOG,利用角的和差关系可得∠FOD=∠AOC,根据对顶角相等,利用等量代换可得∠AOC=∠EOC,即可得答案.
(1)∵∠AOC和∠BOD是对顶角,∠BOD=36°,
∴∠AOC=∠BOD=36°,
∵OG⊥CD,
∴∠COG=∠DOG=90°,
∴∠AOG=∠COG-∠AOC=90°-36°=54°.
(2)OC是∠AOE的角平分线,理由如下:
∵OG是∠AOF的角平分线,
∴∠AOG=∠FOG,
∵∠COG=∠DOG=90°,
∴∠COG-∠AOG=∠DOG-∠FOG,即∠AOC=∠FOD,
∵∠EOC和∠FOD是对顶角,
∴∠EOC=∠FOD,
∴∠AOC=∠EOC,
∴OC是∠AOE的角平分线.

练习册系列答案
相关题目