题目内容
【题目】(中考·安徽)如图,已知反比例函数y=![]() 与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).
与一次函数y=k2x+b的图象交于A(1,8),B(-4,m).

(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)若M(x1,y1),N(x2,y2)是反比例函数y=![]() 的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
的图象上的两点,且x1<x2,y1<y2,指出点M,N位于哪个象限,并简要说明理由.
【答案】(1)k2=2,b=6(2)15(3)点M在第三象限,点N在第一象限
【解析】试题分析:(1)把A(1,8)代入![]() 求得
求得![]() =8,把B(-4,m)代入
=8,把B(-4,m)代入![]() 求得m=-2,把A(1,8)、B(-4,-2)代入
求得m=-2,把A(1,8)、B(-4,-2)代入![]() 求得
求得![]() 、b的值;(2)设直线y=2x+6与x轴的交点为C,可求得OC的长,根据S△ABC=S△AOC+S△BOC即可求得△AOB的面积;(3)由
、b的值;(2)设直线y=2x+6与x轴的交点为C,可求得OC的长,根据S△ABC=S△AOC+S△BOC即可求得△AOB的面积;(3)由![]() <
<![]() 可知有三种情况,①点M、N在第三象限的分支上,②点M、N在第一象限的分支上,③ M在第三象限,点N在第一象限,分类讨论把不合题意的舍去即可.
可知有三种情况,①点M、N在第三象限的分支上,②点M、N在第一象限的分支上,③ M在第三象限,点N在第一象限,分类讨论把不合题意的舍去即可.
试题解析:解:(1)把A(1,8), B(-4,m)分别代入![]() ,得
,得![]() =8,m=-2.
=8,m=-2.
∵A(1,8)、B(-4,-2)在![]() 图象上,
图象上,
∴![]() ,
,
解得, ![]() .
.
(2)设直线y=2x+6与x轴的交点为C,当y=0时,x=-3,
∴OC=3
∴S△ABC=S△AOC+S△BOC=![]()
(3)点M在第三象限,点N在第一象限.
①若![]() <
<![]() <0,点M、N在第三象限的分支上,则
<0,点M、N在第三象限的分支上,则![]() >
>![]() ,不合题意;
,不合题意;
②若0<![]() <
<![]() ,点M、N在第一象限的分支上,则
,点M、N在第一象限的分支上,则![]() >
>![]() ,不合题意;
,不合题意;
③若![]() <0<
<0<![]() ,M在第三象限,点N在第一象限,则
,M在第三象限,点N在第一象限,则![]() <0<
<0<![]() ,符合题意.
,符合题意.

 阅读快车系列答案
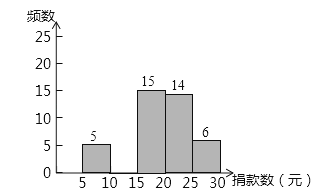
阅读快车系列答案【题目】2015年4月25日,尼泊尔发生了里氏8.1级地震,某中学组织了献爱心捐款活动,该校教学兴趣小组对本校学生献爱心捐款额做了一次随机抽样调查,并绘制了不完整的频数分布表和频数分布直方图(每组含前一个边界值,不含后一个边界值).如图所示:
捐款额(元) | 频数 | 百分比 |
0≤x<5 | 5 | 10% |
10≤x<15 | a | 20% |
15≤x<20 | 15 | 30% |
20≤x<25 | 14 | b |
25≤x<30 | 6 | 12% |
总计 | 100% |
(1)a等于多少?b等于多少?
(2)补全频数分布直方图;
(3)该校共有1600名学生,估计这次活动中爱心捐款额不低于20元的学生有多少人?