题目内容
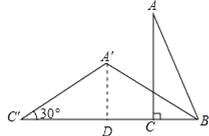
【题目】如图,书桌上的一种新型台历和一块主板AB、一个架板AC和环扣(不计宽度,记为点A)组成,其侧面示意图为△ABC,测得AC⊥BC,AB=5cm,AC=4cm,现为了书写记事方便,须调整台历的摆放,移动点C至C′,当∠C′=30°时,求移动的距离即CC′的长(或用计算器计算,结果取整数,其中![]() =1.732,
=1.732, ![]() =4.583)
=4.583)

【答案】5cm
【解析】试题分析:过点A′作A′D⊥BC′,垂足为D,先在△ABC中,由勾股定理求出BC=3cm,再解Rt△A′DC′,得出A′D=2cm,C′D=2![]() cm,在Rt△A′DB中,由勾股定理求出BD=
cm,在Rt△A′DB中,由勾股定理求出BD=![]() cm,然后根据CC′=C′D+BD﹣BC,将数据代入,即可求出CC′的长.
cm,然后根据CC′=C′D+BD﹣BC,将数据代入,即可求出CC′的长.
试题解析:过点A′作A′D⊥BC′,垂足为D.
在△ABC中,∵AC⊥BC,AB=5cm,AC=4cm,∴BC=3cm.
当动点C移动至C′时,A′C′=AC=4cm.在△A′DC′中,∵∠C′=30°,∠A′DC′=90°,
∴A′D=![]() A′C′=2cm,C′D=
A′C′=2cm,C′D=![]() A′D=2
A′D=2![]() cm.
cm.
在△A′DB中,∵∠A′DB=90°,A′B=5cm,A′D=2cm,∴BD=![]() =
=![]() cm,
cm,
∴CC′=C′D+BD﹣BC=2![]() +
+![]() ﹣3,∵
﹣3,∵![]() =1.732,
=1.732,![]() =4.583,∴CC′=2×1.732+4.583﹣3≈5.
=4.583,∴CC′=2×1.732+4.583﹣3≈5.
故移动的距离即CC′的长约为5cm.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目