��Ŀ����
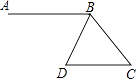
����Ŀ����ͼ������ֽƬABCD�У�AB=![]() ��BC=
��BC=![]() ��ij����С���������ž���ֽƬ���ν������²�����ÿ���۵����չ������
��ij����С���������ž���ֽƬ���ν������²�����ÿ���۵����չ������
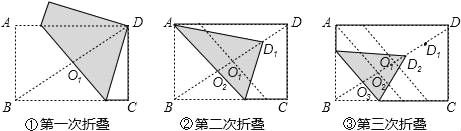
��ͼ������һ�ν�ֽƬ�۵���ʹ��B���D�غϣ��ۺ���BD�����O1����O1D���е�ΪD1��
��ͼ�����ڶ��ν�ֽƬ�۵���ʹ��B���D1�غϣ��ۺ���BD�����O2����O2D3���е�ΪD2��
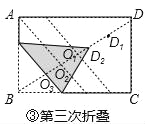
��ͼ���������ν�ֽƬ�۵���ʹ��B���D2�غϣ��ۺ���BD�����O3����O3D2���е�ΪD3��
��
�������ϲ���������ش��������⣺
��1����ͼ����MN���ۺۣ���֤����DA��M�ա�DCN��
��2���ֱ�����߶�BO1��BO2��BO3�ij�����ֱ��д����n���۵���BOn�ij����ú�n��ʽ�ӱ�ʾ����
��3����ͼ�����ڶ����۵�ʱ���ۺ�һ���ᾭ����A����ͨ�������жϣ�
���𰸡�(1)��֤�����̼�������(2)��BOn=![]() ��(3)��֤�����̼�����
��(3)��֤�����̼�����
��������
���������(1)������֤��DM=DN���ٸ���AAS�����жϣ�(2)�������������BO1��BO2��BO3��Ѱ�ҹ��ɺɽ�����⣻(3)�����ۣ��ڶ����۵�ʱ���ۺ�һ���ᾭ����A����AE��BD����ΪE�����BE�ij���֤����E���O2�غϼ��ɣ�
���������(1)����ͼ���У�
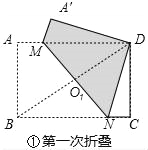
���ı���MNDA�������ı���MNBA���۵õ������ABN=��A��DN=90������BNM=��MND�����ı���ABCD�Ǿ��Σ�
��AD��BC����ADC=90�������BNM=��DMN=��DNM����DM=DN���ߡ�A��DN=��ADC�����A��DM=��NDC��
����DA��M����DCN�У�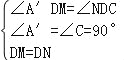 �����DMA��ա�DNC��
�����DMA��ա�DNC��
(2)����ͼ���У�
 ��
��
���ı���ABCD�Ǿ��Σ����C=90����AB=CD=![]() ��BC=AD=
��BC=AD=![]() ����BD=
����BD=![]() =
=![]() =4��
=4��
��BO1=O1D=![]() BD=2=
BD=2=![]() ��BO2=
��BO2=![]() BD1=
BD1=![]() =
=![]() ��BO3=
��BO3=![]() BD2=
BD2=![]() =
=![]() ��
��
��BOn=![]() ��
��
(3)����ͼ���У����ۣ��ڶ����۵�ʱ���ۺ�һ���ᾭ����A��
���ɣ���AE��BD����ΪE��
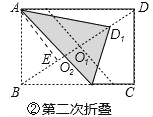
�ߡ�AEB=��BAD=90������ABE=��BAD�����ABE�ס�DBA����![]() =
=![]() ����
����![]() =
=![]() ��
��
��BE=![]() ����BO2=
����BO2=![]() ������E���O2�غϣ����ڶ����۵�ʱ���ۺ�һ���ᾭ����A��
������E���O2�غϣ����ڶ����۵�ʱ���ۺ�һ���ᾭ����A��