题目内容
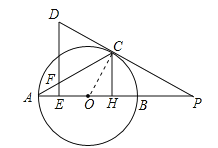
【题目】如图,AB为⊙O直径,过⊙O外的点D作DE⊥OA于点E,射线DC切⊙O于点C、交AB的延长线于点P,连接AC交DE于点F,作CH⊥AB于点H.
(1)求证:∠D=2∠A;
(2)若HB=2,cosD=![]() ,请求出⊙O的半径长.
,请求出⊙O的半径长.
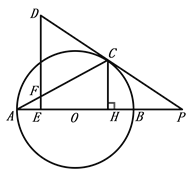
【答案】(1)见解析;(2)5.
【解析】分析:(1)连接OC,根据切线的性质得到∠OCP=90°,根据垂直的定义得到∠DEP=90°,得到∠COB=∠D,根据圆周角定理证明;
(2)设⊙O的半径为r,根据余弦的定义计算即可.
详解:
(1)证明:连接OC,
∵射线DC切⊙O于点C, ∴∠OCP=90°
∵DE⊥AP,∴∠DEP=90°
∴∠P+∠D=90°,∠P+∠COB=90°
∴∠COB=∠D
∵OA=OC, ∴∠A=∠OCA
∵∠COB=∠A+∠OCA ∴∠COB=2∠A
∴∠D=2∠A
(2)解:由(1)可知:∠OCP=90°,∠COP=∠D,
∴cos∠COP=cos∠D=![]() ,
,
∵CH⊥OP,∴∠CHO=90°,
设⊙O的半径为r,则OH=r﹣2.
在Rt△CHO中,cos∠HOC=![]() =
=![]() =
=![]() ,
,
∴r=5

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
【题目】“水是生命之源”,某市自来水公司为了鼓励居民节约用水,规定按以下标准收取水费:
用水量/月 | 单价(元/m3) |
不超过20m3 | 2.8 |
超过20m3的部分 | 3.8 |
另:每立方米用水加收0.2元的城市污水处理费 | |
(1)根据上表,用水量每月不超过20m3,实际每立方米收水费_____元;如果1月份某用户用水量为19m3,那么该用户1月份应该缴纳水费____元;
(2)某用户2月份共缴纳水费80元,那么该用户2月份用水多少m3?
(3)若该用户水表3月份出了故障,只有70%的用水量记入水表中,这样该用户在3月份只缴纳了58.8元水费,问该用户3月份实际应该缴纳水费多少元?