Question

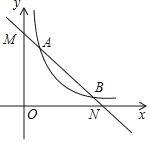
【题目】如图，在平面直角坐标中，点O是坐标原点，一次函数y1=kx+b与反比例函数y2=的图象交于A（1，m）、B（n，1）两点．

（1）求直线AB的解析式；

（2）根据图象写出当y1＞y2时，x的取值范围；

（3）若点P在y轴上，求PA+PB的最小值．

Answer 1

【答案】（1）y=﹣x+4；（2）1＜x＜3；（3）2．

【解析】

（1）依据反比例函数y2= (x＞0)的图象交于A（1，m）、B（n，1）两点，即可得到A（1，3）、B（3，1），代入一次函数y1=kx+b，可得直线AB的解析式；

（2）当1＜x＜3时，正比例函数图象在反比例函数图象的上方，即可得到当y1＞y2时，x的取值范围是1＜x＜3；

（3）作点A关于y轴的对称点C，连接BC交y轴于点P，则PA+PB的最小值等于BC的长，利用勾股定理即可得到BC的长．

（1）A（1，m）、B（n，1）两点坐标分别代入反比例函数y2= (x＞0)，可得

m=3，n=3，

∴A（1，3）、B（3，1），

把A（1，3）、B（3，1）代入一次函数y1=kx+b，可得

，解得，

∴直线AB的解析式为y=-x+4；

（2）观察函数图象，发现：

当1＜x＜3时，正比例函数图象在反比例函数图象的上方，

∴当y1＞y2时，x的取值范围是1＜x＜3．

（3）如图，作点A关于y轴的对称点C，连接BC交y轴于点P，则PA+PB的最小值等于BC的长，

过C作y轴的平行线，过B作x轴的平行线，交于点D，则

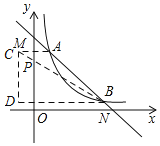
Rt△BCD中，BC=，

∴PA+PB的最小值为2．