题目内容
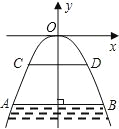
【题目】如图所示，有一座抛物线形拱桥，桥下面在正常水位时，AB宽20 m，水位上升到警戒线CD时，CD到拱桥顶E的距离仅为1 m，这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式；
(2)若洪水到来时，水位以每小时0.3 m的速度上升，从正常水位开始，持续多少小时到达警戒线？
【答案】（1）y=-
x2（2）从正常水位开始，持续10小时到达警戒线
【解析】
（1）首先设所求抛物线的解析式为：y=ax2（a≠0），再根据题意得到C（-5，-1），利用待定系数法即可得到抛物线解析式；
（2）根据抛物线解析式计算出A点坐标，进而得到F点坐标，然后计算出EF的长，再算出持续时间即可．
解：（1）设所求抛物线的解析式为y＝ax2.
∵CD＝10 m，CD到拱桥顶E的距离仅为1 m，
∴C(－5，－1)．
把点C的坐标代入y＝ax2，
得a＝－
，
故抛物线的解析式为y＝－x2.
（2）∵AB宽20 m，
∴可设A(－10，b)．
把点A的坐标代入抛物线的解析式y＝－x2中，
解得b＝－4，
∴点A的坐标为(－10，－4)．
设AB与y轴交于点F，则F(0，－4)，
∴EF＝3 m.
∵水位以每小时0.3 m的速度上升，
∴3÷0.3＝10(时)．
答：从正常水位开始，持续10小时到达警戒线．
【题目】平价商场经销甲、乙两种商品，甲种商品每件售价60元，得利润20元；乙种商品每件进价50元，售价80元．
（1）甲种商品每件进价为_____元，每件乙种商品所赚利润得百分数为_____%；
（2）若该商场同时购进甲、乙两种商品共50件，恰好总进价为2100元，求购进甲种商品多少件？
（3）在“元旦”期间，该商场只对甲、乙两种商品进行如下的优惠促销活动：
打折前一次性购物总金额 | 优惠措施 |
少于等于450 | 不优惠 |
超过450，但不超过600 | 按打九折 |
超过600 | 其中600部分八点二折优惠，超过600的部分打三折优惠 |
按上述优惠条件，若小华一次性购买乙种商品实际付款504元，求小华在该商场购买乙种商品多少件？
