题目内容
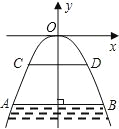
【题目】已知二次函数y＝ax2＋bx＋c的图象如图，对称轴是直线x＝－
，有下列结论：(1)ab＞0；(2)a＋b＋c＜0；(3)b＋2c＜0；(4)a－2b＋4c＞0.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
根据图象知该二次函数的对称轴x=
＜0，所以得到ab＞0；而x=1时，a+b+c＜0；=
，所以2a=3b，x=-1时，a-b+c＞0，所以2a-2b+2c＞0，所以得到b+2c＞0；根据图象-2b＞0，c＞0，a-b+c＞0，b+2c＞0，这几个不等式相加即可得到④正确．
解：①∵=＜0，∴ab＞0，∴该结论正确；
②∵x=1时，y＜0，∴a+b+c＜0正确，∴该结论正确；
③=，∴2a=3b；
又x=-1时，y＞0，∴a-b+c＞0；
∴2a-2b+2c＞0，3b-2b+2c＞0；
∴b+2c＞0，∴该结论错误；
④由图象知a＜0，ab＞0；
∴b＜0；
∴-2b＞0（1）
图象交y轴于正半轴，∴c＞0（2）；
又a-b+c＞0（3），b+2c＞0（4）；
∴（1）+（2）+（3）+（4）得，a-2b+4c＞0，∴该结论正确．
所以正确结论的个数为3．
故选：C．
【题目】小王是“新星厂”的一名工人，请你阅读下列信息：
信息一：工人工作时间：每天上午8：00—12：00，下午14：00—18：00，每月工作25天；
信息二：小王生产甲、乙两种产品的件数与所用时间的关系见下表：
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三：按件计酬，每生产一件甲种产品得1.50元，每生产一件乙种产品得2.80元；
信息四：该厂工人每月收入由底薪和计酬工资两部分构成，小王每月的底薪为1900元．请根据以上信息，解答下列问题：
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟；
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件，则小王该月收入最多是多少元？此时小王生产的甲、乙两种产品分别是多少件？
