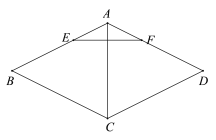
题目内容
【题目】如图,在菱形ABCD中,AC为对角线,点E,F分别在AB,AD上,BE=DF,连接EF.
(1)求证:AC⊥EF;
(2)延长EF交CD的延长线于点G,连接BD交AC于点O,若BD=4,tanG=![]() ,求AO的长.
,求AO的长.
【答案】(1)证明见解析;(2)AO=1。
【解析】
(1)由菱形的性质得出AB=AD,AC平分∠BAD,再根据等腰三角形的三线合一即可;
(2)根据菱形的性质和已知条件得出四边形EBDG为平行四边形,得出∠G=∠ABD,再根据tanG=![]() 即可求出AO的长.
即可求出AO的长.
(1)证明:∵四边形ABCD为菱形 ∴AB=AD,AC平分∠BAD
∵BE=DF, ∴![]() , ∴AE=AF
, ∴AE=AF
∴△AEF是等腰三角形, ∵AC平分∠BAD, ∴AC⊥EF
(2)解:如图2所示:
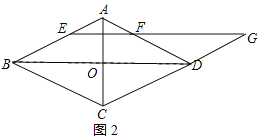
∵四边形ABCD为菱形,∴CG∥AB,BO=![]() BD=2,∵EF∥BD
BD=2,∵EF∥BD
∴四边形EBDG为平行四边形,∴∠G=∠ABD,∴tan∠ABD=tan∠G=![]()
∴tan∠ABD=![]() ,∴AO=1
,∴AO=1

练习册系列答案
相关题目