题目内容
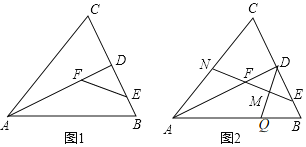
【题目】如图①,△ABC与△ADE均是等腰直角三角形,直角边AC、AD在同一条直线上,点G、H分别是斜边DE、BC的中点,点F为BE的中点,连接GF、GH.
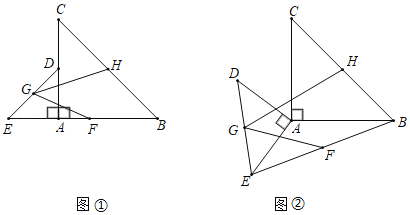
(1)猜想GF与GH的数量关系,请直接写出结论;
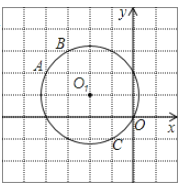
(2)现将图①中的△ADE绕着点A逆时针旋转α(0°<α<90°),得到图②,请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由;
(3)若AD=2,AC=4,将图①中的△ADE绕着点A逆时针旋转一周,直接写出GH的最大值和最小值,并写出取得最值时旋转角的度数.
【答案】(1)![]() ,(2)成立,理由见解析;(3)当点D在线段BA的延长线上时,BD有最大值为AD+AB=6,即GF最小值为3
,(2)成立,理由见解析;(3)当点D在线段BA的延长线上时,BD有最大值为AD+AB=6,即GF最小值为3![]() ,旋转角的度数为90°.
,旋转角的度数为90°.
【解析】
(1)连接CE,FH,BD,延长BD交CE于N,由“SAS”可证△ACE≌△ABD,可得EC=DB,∠ACE=∠ABD,通过证明△GFH是等腰直角三角形,可得结论;
(2)连接CE,FH,BD,延长BD交CE于N,由“SAS”可证△ACE≌△ABD,可得EC=DB,∠ACE=∠ABD,通过证明△GFH是等腰直角三角形,可得结论;
(3)由GH=![]() GF,GF=
GF,GF=![]() BD,可得GF=
BD,可得GF=![]() BD,则当点D在线段AB上时,BD有最小值为AB-AD=2,即GF最小值为
BD,则当点D在线段AB上时,BD有最小值为AB-AD=2,即GF最小值为![]() ,当点D在线段BA的延长线上时,BD有最大值为AD+AB=6,即GF最小值为3
,当点D在线段BA的延长线上时,BD有最大值为AD+AB=6,即GF最小值为3![]() ,即可求解.
,即可求解.
(1)![]() ,
,
理由如下:连接CE,FH,BD,延长BD交CE于N,
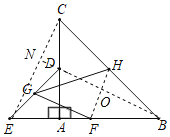
∵△ACB和△ADE是等腰直角三角形,
∴AC=AB,AE=AD,∠CAB=∠EAD=90°.
∴△ACE≌△ABD(SAS),
∴EC=DB,∠ACE=∠ABD.
又∵∠ACE+∠CEA=90°,
∴∠ABD+∠CEA=90°,
∴∠BNE=90°,
∵点G、F、H分别为ED、EB、BC的中点,
∴GF=![]() BD,GF∥BD,FH=
BD,GF∥BD,FH=![]() EC,FH∥EC.
EC,FH∥EC.
∴CF=FH,∠ENB=∠FOB=∠GFH=90°,
∴△GFH是等腰直角三角形,
∴GH=![]() GF;
GF;
(2)连接EC,FH,BD,EC交BD于点I,交GF于点M,FH交BD于N,
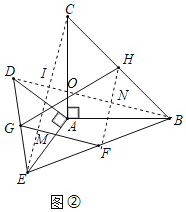
∵△ACB和△ADE是等腰直角三角形,
∴AC=AB,AE=AD,∠CAB=∠EAD=90°,
∴∠CAB+∠DAC=∠EAD+∠DAC.
∴∠EAC=∠BAD,
∴△ACE≌△ABD(SAS),
∴EC=DB,∠ACE=∠ABD.
又∵∠AOB=∠COI,
∴∠OIC=∠BAO=90°,
∵点G、F、H分别为ED、EB、BC的中点,
∴GF=![]() BD,GF∥BD,FH=
BD,GF∥BD,FH=![]() EC,FH∥EC.
EC,FH∥EC.
∴GF=FH.四边形FMIN是平行四边形,
∴∠MFN=∠MIN=180°﹣90°=90°,
∴△GFH是等腰直角三角形,
∴![]() ;
;
(3)∵GH=![]() GF,GF=
GF,GF=![]() BD,
BD,
∴GF=![]() BD,
BD,
∴当BD有最大值时,GF有最大值,当BD有最小值时,GF有最小值,
∴当点D在线段AB上时,BD有最小值为AB﹣AD=2,即GF最小值为![]() ,旋转角的度数为270°;
,旋转角的度数为270°;
当点D在线段BA的延长线上时,BD有最大值为AD+AB=6,即GF最小值为3![]() ,旋转角的度数为90°.
,旋转角的度数为90°.

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案