Question

【题目】定义：有两个相邻内角互余的四边形称为邻余四边形，这两个角的夹边称为邻余线．

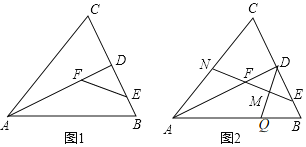
（1）如图1，在△ABC中，AB＝AC，AD是△ABC的角平分线，E，F分别是BD，AD上的点．求证：四边形ABEF是邻余四边形．

（2）如图2，在（1）的条件下，取EF中点M，连结DM并延长交AB于点Q，延长EF交AC于点N．若N为AC的中点，DE＝2BE，QB＝3，求邻余线AB的长．

Answer 1

【答案】（1）详见解析；（2）10．

【解析】

（1）由等腰三角形的三线合一定理先证AD⊥BC，再证∠DAB+∠DBA＝90°，由邻余四边形定义即可判定；

（2）由等腰三角形的三线合一定理先证BD＝CD，推出CE＝5BE，再证明△DBQ∽△ECN，推出，即可求出NC，AC，AB的长度．

解：（1）∵AB＝AC，AD是△ABC的角平分线，

∴AD⊥BC，

∴∠ADB＝90°，

∴∠DAB+∠DBA＝90°，

∴∠FAB与∠EBA互余，

∴四边形ABEF是邻余四边形；

（2）∵AB＝AC，AD是△ABC的角平分线，

∴BD＝CD，

∵DE＝2BE，

∴BD＝CD＝3BE，

∴CE＝CD+DE＝5BE，

∵∠EDF＝90°，点M是EF的中点，

∴DM＝ME，

∴∠MDE＝∠MED，

∵AB＝AC，

∴∠B＝∠C，

∴△DBQ∽△ECN，

∴，

∵QB＝3，

∴NC＝5，

∵AN＝CN，

∴AC＝2CN＝10，

∴AB＝AC＝10．