题目内容
【题目】已知⊙O1经过A(-4,2)、B(-3,3)、C(-1,-1)、O(0,0)四点,一次函数y=-x-2的图象是直线l,直线l与y轴交于点D.
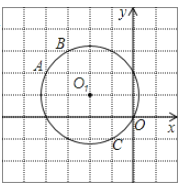
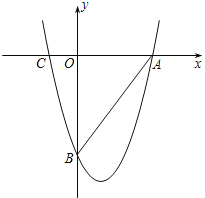
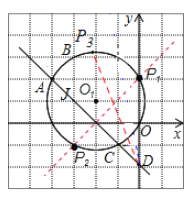
(1)在右边的平面直角坐标系中画出直线l,则直线l与⊙O1的交点坐标为 ;
(2)若⊙O1上存在点P,使得△APD为等腰三角形,则这样的点P有 个,试写出其中一个点P坐标为 .
【答案】(1)图见解析,
直线l与⊙O1的交点坐标为(-4,2),(-1,1);
(2)3,(-3,-1)或(0,2)
【解析】
(1)要先在坐标系上找到这些点,再画过这些点的图象;
(2)根据线段垂直平分线上的两点到线段两端的距离相等.作AD的垂直平分线,与圆的交点且是整点的点的坐标就是所求的坐标;
先在坐标系中找到A(-4,2),B(-3,3),C(-1,-1),O(0,0)的坐标,然后画圆,过此四点.一次函数y=-x-2,当x=0时,y=-2;当y=0时,x=-2,从坐标系中先找出这两点,画过这两点的直线.即是一次函数y=-x-2的图象.
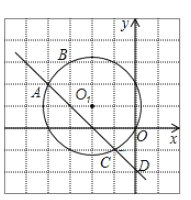
该直线与圆的交点,从图中可看出是(-4,2)(-1,-1);
(2)作AD的垂直平分线,与圆的交点是所求的坐标(根据垂直平分线上的两点到线段两端的距离相等),以点D为圆心,以DA为半径画弧,弧与⊙O1的交点是A点和P3点,从图中可以看出这样的点有三个坐标,可求的其中一个是(-3,-1)

练习册系列答案
相关题目