题目内容
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是【 】


A. | B. | C. | D. |
B。
分别求出点P在DE、AD、AB上运动时,S与t的函数关系式,结合选项即可得出答案:
根据题意得:当点P在ED上运动时,S=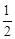 BC•PE=2t;
BC•PE=2t;
当点P在DA上运动时,此时S=8;
当点P在线段AB上运动时,S=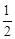 BC(AB+AD+DE-t)=5-
BC(AB+AD+DE-t)=5-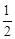 t。
t。
结合选项所给的函数图象,可得B选项符合。故选B。
根据题意得:当点P在ED上运动时,S=
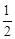 BC•PE=2t;
BC•PE=2t;当点P在DA上运动时,此时S=8;
当点P在线段AB上运动时,S=
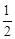 BC(AB+AD+DE-t)=5-
BC(AB+AD+DE-t)=5-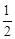 t。
t。结合选项所给的函数图象,可得B选项符合。故选B。

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目

 地逆流而上,前往
地逆流而上,前往 地营救受困群众,途经
地营救受困群众,途经 地时,由所携带的救生艇将
地时,由所携带的救生艇将 (千米)和冲锋舟出发后所用时间
(千米)和冲锋舟出发后所用时间 (分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
(分)之间的函数图象如图所示.假设营救群众的时间忽略不计,水流速度和冲锋舟在静水中的速度不变.
 ,假设群众上下船的时间不计,求冲锋舟在距离
,假设群众上下船的时间不计,求冲锋舟在距离


 ,
, ),B(
),B( ,
, ),且
),且