题目内容
图为一位旅行者在早晨8时从城市出发到郊外所走的路程S(单位:千米)与时间t(单位:时)的变量关系的图象。根据图象回答问题:

(1)在这个变化过程中,自变量是____,因变量是______。
(2)9时,10时30分,12时所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?

(1)在这个变化过程中,自变量是____,因变量是______。
(2)9时,10时30分,12时所走的路程分别是多少?
(3)他休息了多长时间?
(4)他从休息后直至到达目的地这段时间的平均速度是多少?
1、(1)时间,路程。……(2’), (2)4千米,9千米,15千米。…….(5’)
(3)0.5小时。…….(6’) (4) 4千米/小时。……(8’)
(3)0.5小时。…….(6’) (4) 4千米/小时。……(8’)
(1)变量应看横轴和纵轴表示的量,自变量是横轴表示的量,因变量是纵轴表示的量.
(2)看相对应的y的值即可.
(3)休息时,时间在增多,路程没有变化,表现在函数图象上是与x轴平行.
(4)这段时间的平均速度=这段时间的总路程÷这段时间
(2)看相对应的y的值即可.
(3)休息时,时间在增多,路程没有变化,表现在函数图象上是与x轴平行.
(4)这段时间的平均速度=这段时间的总路程÷这段时间

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 x+b和y=
x+b和y= x的图象交于点P
x的图象交于点P , 则根据图象可得,关于
, 则根据图象可得,关于  的二元一次方程组的解是____________.
的二元一次方程组的解是____________. 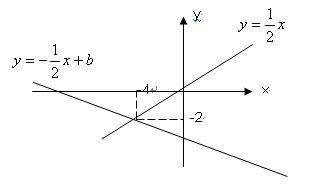
 是过点(3,0),并且垂直于
是过点(3,0),并且垂直于 轴,从2,3,4,5这四个数中,任取两个数
轴,从2,3,4,5这四个数中,任取两个数 和
和 (
( ),构成函数
),构成函数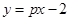 和
和 ,使两个函数图象的交点在直线
,使两个函数图象的交点在直线 )共有()
)共有()




 (件)与第x天的关系式为
(件)与第x天的关系式为 件与第x天的关系如图所示
件与第x天的关系如图所示

 的图象不经过的象限是( )
的图象不经过的象限是( )