题目内容
【题目】正方形ABCD的四个顶点都在⊙O上，E是⊙O上的一点．
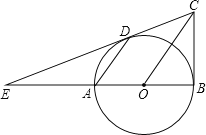
（1）如图①，若点E在
上，F是DE上的一点，DF=BE．求证：△ADF≌△ABE；
（2）在（1）的条件下，小明还发现线段DE、BE、AE之间满足等量关系：DE﹣BE=
AE．请你说明理由；
（3）如图②，若点E在
上．写出线段DE、BE、AE之间的等量关系．（不必证明）
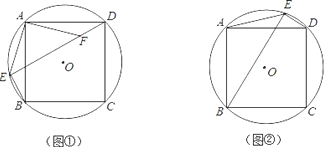
第26题
【答案】（1）证明见解析；（2）理由见解析；（3）BE-DE=
AE．
【解析】
（1）中易证AD=AB，EB=DF，所以只需证明∠ADF=∠ABE，利用同弧所对的圆周角相等不难得出，从而证明全等；
（2）中易证△AEF是等腰直角三角形，所以EF=AE，所以只需证明DE-BE=EF即可，由BE=DF不难证明此问题；
（3）类比（2）不难得出（3）的结论．
（1）如图：
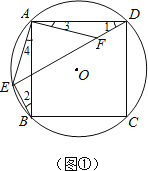
在正方形ABCD中，AB=AD，
∵∠1和∠2都对
，
∴∠1=∠2，
在△ADF和△ABE中，
，
∴△ADF≌△ABE（SAS）；
（2）由（1）有△ADF≌△ABE，
∴AF=AE，∠3=∠4，
在正方形ABCD中，∠BAD=90°，
∴∠BAF+∠3=90°，
∴∠BAF+∠4=90°，
∴∠EAF=90°，
∴△EAF是等腰直角三角形，
∴EF2=AE2+AF2，
∴EF2=2AE2，
∴EF=AE，
即DE-DF=AE，
∴DE-BE=AE；
（3）BE-DE=AE．理由如下：
在BE上取点F，使BF=DE，连接AF，
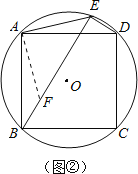
易证△ADE≌△ABF，
∴AF=AE，∠DAE=∠BAF，
在正方形ABCD中，∠BAD=90°，
∴∠BAF+∠DAF=90°，
∴∠DAE+∠DAF=90°，
∴∠EAF=90°，
∴△EAF是等腰直角三角形，
∴EF2=AE2+AF2，
∴EF2=2AE2，
∴EF=AE，
即BE-BF=AE，
∴BE-DE=AE．
