Question

【题目】如图所示，在直角坐标系xOy中，一次函数y1=k1x+b（k≠0）的图象与反比例函数（x＞0）的图象交于A（1，4），B（3，m）两点．

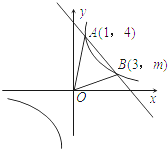
（1）试确定上述反比例函数和一次函数的表达式；

（2）在第一象限内，x取何值时，一次函数的函数值大于反比例函数的函数值；

（3）求△AOB的面积．

Answer 1

【答案】（1）y1=﹣x+（2）x取1＜x＜3 （3）

【解析】

试题（1）把A（1，4）代入数即可求出反比例函数的解析式，把B的坐标代入即可求出B的坐标，把A、B的坐标代入一次函数的解析式，得出方程组，求出方程组的解，即可得出一次函数的解析式；

（2）根据图象和A、B的坐标即可得出答案；

（3）过A作AE⊥ON于E，过B作BF⊥OM于F，求出M、N的坐标，根据S△AOB=S△NOM﹣S△AON﹣S△BOM代入即可求出△AOB的面积．

解：（1）把A（1，4）代入数（x＞0）得：4=，

解得：k2=4，

即反比例函数的解析式是：y2=，

把B（3，m）代入上式得：m=，

即B（3，），

把A、B的坐标代入y1=k1x+b（k≠0）得：

，

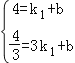解得：k=﹣，b=，

∴一次函数的解析式是：y1=﹣x+；

（2）从图象可知：在第一象限内，x取1＜x＜3时，一次函数的函数值大于反比例函数的函数值；

（3）过A作AE⊥ON于E，过B作BF⊥OM于F，

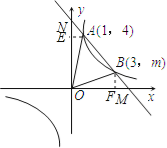
∵A（1，4），B（3，），

∴AE=1，BF=，

∵设直线AB（y1=﹣x+）交y轴于N，交x轴于M，

当x=0时，y=，

当y=0时，x=4，

即ON=，OM=4，

∴S△AOB=S△NOM﹣S△AON﹣S△BOM

=××4﹣××1﹣×4×

=．