题目内容
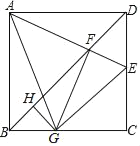
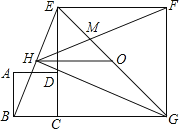
【题目】如图l,在![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() 是线段
是线段![]() 上的点(与
上的点(与![]() ,
,![]() 不重合),
不重合),![]() ,
,![]() ,连结
,连结![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
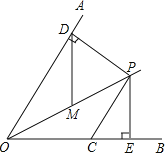
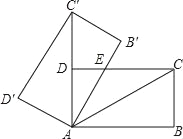
(2)如图2,若将![]() 绕点
绕点![]() 旋转,使边
旋转,使边![]() 在
在![]() 的内部,延长
的内部,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
①求证:![]() ;
;
②当![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() 时,请求出
时,请求出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)通过证明△EAB≌△FAB,即可得到BE=BF;
(2)①首先证明△AEB≌△AFC,由相似三角形的性质可得:∠EBA=∠FCA,进而可证明△AGC∽△KGB;
②根据题意,可分类讨论求值即可.
(1)∵AB=AC,AO⊥BC,
∴∠OAC=∠OAB=45°,
∴∠EAB=∠EAF-∠BAF=45°,
∴∠EAB=∠BAF=45°,
在△EAB和△FAB中,
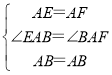 ,
,
∴△EAB≌△FAB(SAS),
∴BE=BF;
(2)①∵∠BAC=90°,∠EAF=90°,
∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC,
在△AEB和△AFC中,
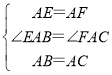 ,
,
∴△AEB≌△AFC(SAS),
∴∠EBA=∠FCA,
又∵∠KGB=∠AGC,
∴△AGC∽△KGB;
②当∠EBF=90°时,
∵EF=BF,
∴∠FEB=∠EBF=90°(不符合题意),
当∠BEF=90°,且EF=BF时,
∴∠FEB=∠EBF=90°(不符合题意),
当∠EFB=90°,且EF=BF时,如下图,
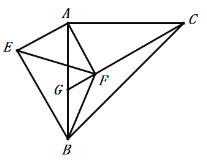
∴∠FEB=∠FBE=45°,
∵![]() ,
,![]() ,
,
∴∠AFE=∠AEF=45°,
∴∠AEB=∠AEF+∠FEB=45°+ 45°=90°,
不妨设![]() ,则BF= EF=
,则BF= EF=![]() ,BE=
,BE=![]() ,
,
在Rt△ABE中,∠AEB =90°,![]() ,BE
,BE![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上,![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目