题目内容
【题目】已知四边形ABCD,![]() 轴,点
轴,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 是四边形ABCD边上的一个动点.
是四边形ABCD边上的一个动点.
(1)若四边形ABCD是菱形,求点![]() 的坐标.
的坐标.
(2)如图1,若![]() ,点
,点![]() 在第四象限内
在第四象限内
①若点![]() 在边
在边![]() ,
,![]() 上,点
上,点![]() 关于坐标轴对称的点
关于坐标轴对称的点![]() 落在直线
落在直线![]() 上,求点
上,求点![]() 的坐标.
的坐标.
②若点![]() 在边
在边![]() ,
,![]() ,
,![]() 上,点
上,点![]() 是
是![]() 与
与![]() 轴的交点,如图2,过点
轴的交点,如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,过点
,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,它们相交于点
,它们相交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,当点
翻折,当点![]() 的对应点落在坐标轴上时,求点
的对应点落在坐标轴上时,求点![]() 的坐标.(直接写出答案)
的坐标.(直接写出答案)


【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() 或
或![]() 或
或![]() ,②
,②![]() 或
或![]() 或
或 或
或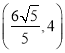
【解析】
(1)由![]() 轴,得点
轴,得点![]() 的纵坐标为-4,再求AD的长,即可求出点
的纵坐标为-4,再求AD的长,即可求出点![]() 的坐标
的坐标
;
(2) ①分两种情况讨论,当点![]() 在边
在边![]() 上时和当点
上时和当点![]() 在边
在边![]() 上时,分别求解即可;
上时,分别求解即可;
②分三种情况讨论,当点![]() 在线段
在线段![]() 上时,当点
上时,当点![]() 在
在![]() 上时,当点
上时,当点![]() 在线段
在线段![]() 上时,分别求解即可.
上时,分别求解即可.
解:(1)∵![]() 轴,
轴,
∴点![]() 的纵坐标为-4,
的纵坐标为-4,
∵点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴AD=![]() =
= ![]() ,
,
∴点![]() 的横坐标为1+
的横坐标为1+![]() ,
,
点![]() 的坐标为
的坐标为![]() ;
;
(2)①当点![]() 在边
在边![]() 上时,
上时,
∵直线![]() 的解析式为
的解析式为![]() ,
,
设![]() ,且
,且![]() ,
,
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
解得![]() ,
,
此时![]() .
.
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上时,
上时,
∴![]() ,解得
,解得![]() ,此时
,此时![]()
②当点![]() 在边
在边![]() 上时,设
上时,设![]() 且
且![]() ,
,
若等![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,解得
,解得![]() ,此时
,此时![]() ,
,
若点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
解得![]() .此时
.此时![]() ,
,
综上所述,点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
(3)①如图1中,

当点![]() 在线段
在线段![]() 上时,设
上时,设![]() .
.
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]()
∴![]() ,
,
解得![]() ,
,
∴
根据对称性可知,![]() 也满足条件.
也满足条件.
②如图2中,

当点![]() 在
在![]() 上时,易知四边形
上时,易知四边形![]() 是正方形,边长为2,此时
是正方形,边长为2,此时![]() .
.
③如图3中,

当点![]() 在线段
在线段![]() 上时,设
上时,设![]() 交
交![]() 轴于
轴于![]() .易证
.易证![]() ,推出
,推出![]() ,设
,设![]() .
.
∵直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() ,
,
在![]() 中,有
中,有![]() ,解得
,解得![]() ,
,
∴![]() .
.
点![]() 坐标为
坐标为![]() 或
或![]() 或
或 或
或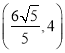 .
.

练习册系列答案
相关题目







