题目内容
【题目】如图,△ABC的两条高线BD,CE相交于点F,已知∠ABC=60°,AB=10,CF=EF,则△ABC的面积为( ) 
A.20 ![]()
B.25 ![]()
C.30 ![]()
D.40 ![]()
【答案】A
【解析】解:连接AF延长AF交BC于G.设EF=CF=x, ∵BD、CE是高,
∴AG⊥BC,
∵∠ABC=60°,∠AGB=90°,
∴∠BAG=30°,
在Rt△AEF中,∵EF=x,∠EAF=30°,∴AE= ![]() x,
x,
在Rt△BCE中,∵EC=2x,∠CBE=60°,∴BE= ![]() x.
x.
∴ ![]() x+
x+ ![]() x=10,
x=10,
∴x=2 ![]() ,
,
∴CE=4 ![]() ,
,
∴S△ABC= ![]() ABCE=
ABCE= ![]() ×10×4
×10×4 ![]() =20
=20 ![]() .
.
故选A.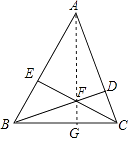
连接AF延长AF交BC于G.设EF=CF=x,连接AF延长AF交BC于G.设EF=CF=x,因为BD、CE是高,所以AG⊥BC,由∠ABC=60°,∠AGB=90°,推出∠BAG=30°,在Rt△AEF中,由EF=x,∠EAF=30°可得AE= ![]() x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE=
x,在Rt△BCE中,由EC=2x,∠CBE=60°可得BE= ![]() x.可得
x.可得 ![]() x+
x+ ![]() x=10,解方程即可解决问题.
x=10,解方程即可解决问题.

练习册系列答案
相关题目