题目内容
【题目】在直角三角形△ABC中,∠C=90°,AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,AD、BE相交于点F,过点D作DG∥AB,过点B作BG⊥DG交DG于点G.下列结论:①∠AFB=135°;②∠BDG=2∠CBE;③BC平分∠ABG;④∠BEC=∠FBG.其中正确的是_________.(填序号)

【答案】①②④
【解析】
根据三角形内角和定理以及角平分线的定义即可判断①;根据平行线的性质和已知条件即可判断②;由∠ABC的度数不确定即可判断③;根据余角的性质和角平分线的定义即可判断④,进而可得结论.
解:∵AD平分∠BAC交BC于点D,BE平分∠ABC交AC于点E,
∴∠BAF=![]() ∠BAC,∠ABF=
∠BAC,∠ABF=![]() ∠ABC,
∠ABC,
∵∠C=90°,
∴∠ABC+∠BAC=90°,
∴∠BAF+∠ABF=45°,
∴∠AFB=135°,故①正确;
∵DG∥AB,
∴∠BDG=∠ABC=2∠CBE,故②正确;
∵∠ABC的度数不确定,
∴BC平分∠ABG不一定成立,故③错误;
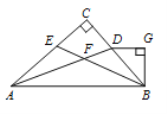
∵BE平分∠ABC,
∴∠ABF=∠CBE,
又∵∠C=∠ABG=90°,
∴∠BEC+∠CBE=90°,∠ABF+∠FBG=90°,
∴∠BEC=∠FBG,故④正确.
故答案为:①②④.

练习册系列答案
相关题目