题目内容
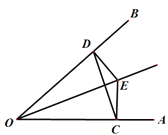
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D,连接C、D.
(1)求证:OC=OD;
(2)请确定射线OE与线段CD 的位置关系,并说明理由.
【答案】见解析
【解析】试题分析:(1)由已知条件易得∠EDO=∠ECO=90°,DE=CE,从而得到∠EDC=∠ECD,进一步得到∠ODC=∠OCD,最后可由“等边对等角”得到OC=OD(也可通过证△ODE≌△OCE来证明OC=OD);
(2)由(1)可知OC=OD,DE=CE,从而可证得OE是CD的垂直平分线得到结论.
试题解析:(1)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴ DE=CE,∠EDO=∠ECO=90°,
∴∠EDC=∠ECD,
∴∠EDO-∠EDC=∠ECO-∠ECD,即∠ODC=∠OCD,
∴OC=OD.
(2) 射线OE垂直平分线段CD,理由如下:
由(1)可得:DE=CE,OC=OD
∴点E和点O都在线段CD的垂直平分线上,
∴射线OE垂直平分线段CD.
∴ 射线OE与线段CD的位置关系是互相垂直.

练习册系列答案
相关题目