题目内容
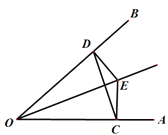
【题目】如图,在平面直角坐标系中,△AOB的顶点O为坐标原点,点A的坐标为(4,0),点B的坐标为(0,1),点C为边AB的中点,正方形OBDE的顶点E在x轴的正半轴上,连接CO,CD,CE.
(1)线段OC的长为 ;
(2)求证:△CBD≌△COE;
(3)将正方形OBDE沿x轴正方向平移得到正方形O1B1D1E1,其中点O,B,D,E的对应点分别为点O1,B1,D1,E1,连接CD,CE,设点E的坐标为(a,0),其中a≠2,△CD1E1的面积为S.
①当1<a<2时,请直接写出S与a之间的函数表达式;
②在平移过程中,当S=![]() 时,请直接写出a的值.
时,请直接写出a的值.

【答案】(1)![]() ;(2)详见解析;(3)①S=﹣
;(2)详见解析;(3)①S=﹣![]() a+1;②当S=
a+1;②当S=![]() 时,a=
时,a=![]() 或
或![]() .
.
【解析】
试题分析:(1)由点A的坐标为(4,0),点B的坐标为(0,1),根据勾股定理求得AB的长,再由点C为边AB的中点,根据直角三角形斜边的中线等于斜边的一半,即可求得线段OC的长;(2)由四边形OBDE是正方形,直角三角形斜边的中线等于斜边的一半,易得BD=OE,BC=OC,∠CBD=∠COE,即可证得:△CBD≌△COE;(3)①首先根据题意画出图形,然后过点C作CH⊥D1E1于点H,可求得△CD1E1的高与底,继而求得答案;
②分别从1<a<2与a>2去分析求解即可求得答案.
试题解析:(1)∵点A的坐标为(4,0),点B的坐标为(0,1),
∴OA=4,OB=1,
∵∠AOB=90°,
∴AB=![]() ,
,
∵点C为边AB的中点,
∴OC=![]() AB=
AB=![]() ;
;
(2)证明:∵∠AOB=90°,点C是AB的中点,
∴OC=BC=![]() AB,
AB,
∴∠CBO=∠COB,
∵四边形OBDE是正方形,
∴BD=OE,∠DBO=∠EOB=90°,
∴∠CBD=∠COE,
在△CBD和△COE中,
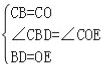 ,
,
∴△CBD≌△COE(SAS);
(3)①解:过点C作CH⊥D1E1于点H,
∵C是AB边的中点,
∴点C的坐标为:(2,![]() )
)
∵点E的坐标为(a,0),1<a<2,
∴CH=2﹣a,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1×(2﹣a)=﹣
×1×(2﹣a)=﹣![]() a+1;
a+1;
②当1<a<2时,S=﹣![]() a+1=
a+1=![]() ,
,
解得:a=![]() ;
;
当a>2时,同理:CH=a﹣2,
∴S=![]() D1E1CH=
D1E1CH=![]() ×1×(a﹣2)=
×1×(a﹣2)=![]() a﹣1,
a﹣1,
∴S=![]() a﹣1=
a﹣1=![]() ,
,
解得:a=![]() ,
,
综上可得:当S=![]() 时,a=
时,a=![]() 或
或![]() .
.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案