题目内容
【题目】如果等腰三角形的一边长为8，另一边长为10，那么连结这个三角形各边的中点所成的三角形的周长为 _______.
【答案】13或14
【解析】
作图分析，根据中位线定理得出△DEF的周长等于△ABC的周长的一半，再分两种情况讨论，从而求得其周长．
解：如图，△ABC中，AB=AC=8cm，BC=10cm，D、E、F分别是边AB、BC、AC的中点．
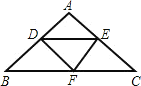
求△DEF的周长．
①∵AB=AC=8，BC=10，D、E、F分别是边AB、BC、AC的中点，
∴DE=
BC，DF=AC，EF=AB，
∴△DEF的周长=DE+DF+EF=（8+8+10）=13，
②∵AB=AC=10，BC=8，D、E、F分别是边AB、BC、AC的中点，
∴DE=BC，DF=AC，EF=AB，
∴△DEF的周长=DE+DF+EF=（8+10+10）=14，
故答案为：13或14．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
