题目内容
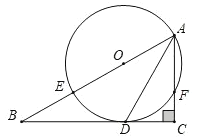
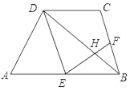
【题目】已知:如图,在四边形![]() 中,
中,![]()
![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为;同时
方向匀速运动,速度为;同时![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向在
方向在![]() 的延长线上匀速运动,速度为
的延长线上匀速运动,速度为![]() ;当点
;当点![]() 到达点
到达点![]() 时,点
时,点![]() 停止运动.过点
停止运动.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
![]() 连接
连接![]() ,当
,当![]() 为何值时,
为何值时,![]()
![]() 设四边形
设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
![]() 在运动过程中,是否存在某一时刻
在运动过程中,是否存在某一时刻![]() ,使四边形
,使四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
![]() 在运动过程中,是否存在某一时刻
在运动过程中,是否存在某一时刻![]() , 使
, 使![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

【答案】(1)当![]() 为
为![]() 时,
时,![]() (2)
(2)![]() ;(3)当
;(3)当![]() 时,四边形
时,四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]() ;(4)当
;(4)当![]() 为
为![]() 时,
时,![]()
【解析】
(1)若![]() ,易得四边形
,易得四边形![]() 是平行四边形,用含t的代数式表示AP和DQ的长度,根据平行四边形的性质得AP=DQ,列方程求解即可.
是平行四边形,用含t的代数式表示AP和DQ的长度,根据平行四边形的性质得AP=DQ,列方程求解即可.
(2)过点![]() 作
作![]() 垂足为
垂足为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,延长
,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .则四边形
.则四边形![]() 是矩形,求得BF=4,AF=6,DF=8,MN=8,由PE∥BD得
是矩形,求得BF=4,AF=6,DF=8,MN=8,由PE∥BD得![]() ,求得AE=AP=2t,证明
,求得AE=AP=2t,证明![]() ,根据相似三角形的性质得
,根据相似三角形的性质得![]() ,
,![]() ,根据
,根据![]() 代入数据整理即可.
代入数据整理即可.
(3)假设存在某一时刻 ![]() 满足条件,列出方程
满足条件,列出方程![]() 求解即可.
求解即可.
(4)若存在某一时刻![]() ,使
,使![]() ,垂足为
,垂足为![]() ,利用条件证得
,利用条件证得![]() ,得到DE=DQ,代入数据求解即可.
,得到DE=DQ,代入数据求解即可.
解:![]() 若
若![]()
![]()
![]() 四边形
四边形![]() 是平行四边形
是平行四边形
![]()
![]()
解得![]()
![]() 当
当![]() 为
为![]() 时,
时,![]()
![]()
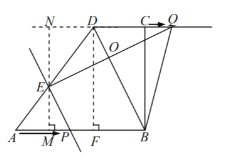
过点![]() 作
作![]() 垂足为
垂足为![]() ,
,
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,
,
延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
![]()
![]()
![]()
![]()
![]() 四边形
四边形![]() 是矩形
是矩形
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 与的函数关系式是
与的函数关系式是![]()
![]() 假设存在某一时刻
假设存在某一时刻 ![]() ,
,
四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]()
则![]()
解得,![]() (不合题意,舍去)
(不合题意,舍去)
答:当![]() 时,四边形
时,四边形![]() 的面积为四边形
的面积为四边形![]() 面积的
面积的![]()
![]() 若存在某一时刻
若存在某一时刻![]() ,使
,使![]() ,垂足为
,垂足为![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 当
当![]() 为
为![]() 时,
时,![]()

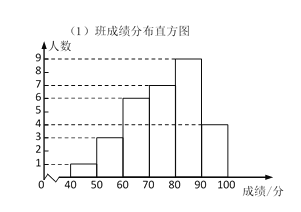
【题目】生活垃圾分类回收是实现垃圾减量化和资源化的重要途径和手段.为了解2019年某市第二季度日均可回收物回收量情况,随机抽取该市2019年第二季度的![]() 天数据,整理后绘制成统计表进行分析.
天数据,整理后绘制成统计表进行分析.
日均可回收物回收量(千吨) |
|
|
|
|
| 合计 |
频数 | 1 | 2 |
| 3 |
| |
频率 | 0.05 | 0.10 |
| 0.15 | 1 |
表中![]() 组的频率
组的频率![]() 满足
满足![]() .
.
下面有四个推断:
①表中![]() 的值为20;
的值为20;
②表中![]() 的值可以为7;
的值可以为7;
③这![]() 天的日均可回收物回收量的中位数在
天的日均可回收物回收量的中位数在![]() 组;
组;
④这![]() 天的日均可回收物回收量的平均数不低于3.
天的日均可回收物回收量的平均数不低于3.
所有合理推断的序号是( )
A.①②B.①③C.②③④D.①③④
【题目】某体育用品商店购进了足球和排球共20个,一共花了1360元,进价和售价如表:
足球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(l)购进足球和排球各多少个?
(2)全部销售完后商店共获利润多少元?