题目内容
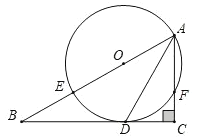
【题目】如图,E是![]() 的斜边AB上一点,以AE为直径的
的斜边AB上一点,以AE为直径的![]() 与边BC相切于点D,交边AC于点F,连结AD.
与边BC相切于点D,交边AC于点F,连结AD.
(1)求证:AD平分![]() .
.
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连结OD,由切线的性质及∠C=90°可得OD∥AC,进而得∠CAD=∠ODA,再由OA=OD得∠OAD=∠ODA,等量代换即可得证;
(2)先由∠CAD=25°求得∠EOF=100°,再利用弧长公式计算即可.
(1)如图,连结OD.
∵⊙O与边BC相切于点D,
∴OD⊥BC,
∴∠ODB=90°.
∵∠C=90°,
∴∠C=∠ODB=90°,
∴OD∥AC,
∴∠CAD=∠ODA.
∵OA=OD,
∴∠OAD=∠ODA,
∴∠OAD=∠CAD.
∴AD平分∠BAC.
(2)如图,连结OF.
∵AD平分∠BAC,且∠CAD=25°,
∴![]() ,
,
∴∠EOF=100°,
∴![]() 的长为
的长为![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班![]() 名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
金额/元 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 18 | 10 | 8 | 2 |
A.平均数为![]() 元B.众数为
元B.众数为![]() 元C.中位数为
元C.中位数为![]() 元D.极差为
元D.极差为![]() 元
元
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 | 日 | 一 | 二 | 三 | 四 | 五 | 六 |
个数 | 11 | 12 | 13 | 12 |
其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()