题目内容
 如图,在平行四边形ABCD中,E为BC边上一点,且∠AED=∠B,在DE上取一点F,使AF=AE.
如图,在平行四边形ABCD中,E为BC边上一点,且∠AED=∠B,在DE上取一点F,使AF=AE.
(1)请直接写出图中所有相似的三角形(不必证明);
(2)若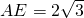 ,BC=3BE,求DE•DF的值.
,BC=3BE,求DE•DF的值.
(可以直接使用第(1)小题结论).
解:(1)△ABE∽△DEA,△AFD∽△DCE.
(2)∵BC=3BE,
∴设BE=x,则BC=3x,
∴AD=3x,EC=2x,
由△ABE∽△DEA,得: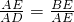 ,
,
∵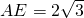 ,
,
∴ ,
,
∴x=2,
又由△AFD∽△DCE,
得DE•DF=AD•EC=3x×2x=6x2,
∴DE•DF=24.
故答案为:24.
分析:(1)根据相似三角形的判定方法可直接得出答案.
(2)利用△ABE∽△DEA,将已知数值代入求得BE,再利用△AFD∽△DCE即可得出DE•DF的值.
点评:此题主要考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握,此题的关键是利用相似三角形的性质,先求出BE,然后再求DE•DF的值,总之难度不大,是一道基础题.
(2)∵BC=3BE,
∴设BE=x,则BC=3x,
∴AD=3x,EC=2x,
由△ABE∽△DEA,得:
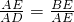 ,
,∵
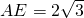 ,
,∴
 ,
,∴x=2,
又由△AFD∽△DCE,
得DE•DF=AD•EC=3x×2x=6x2,
∴DE•DF=24.
故答案为:24.
分析:(1)根据相似三角形的判定方法可直接得出答案.
(2)利用△ABE∽△DEA,将已知数值代入求得BE,再利用△AFD∽△DCE即可得出DE•DF的值.
点评:此题主要考查学生对相似三角形的判定与性质和平行四边形的性质的理解和掌握,此题的关键是利用相似三角形的性质,先求出BE,然后再求DE•DF的值,总之难度不大,是一道基础题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
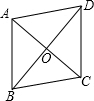 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有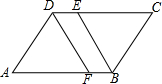 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.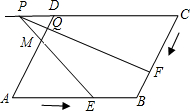 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.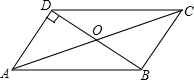 (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为