题目内容
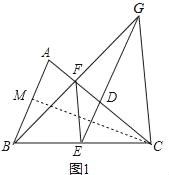
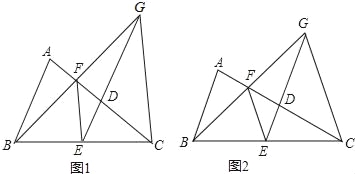
【题目】如图,已知等腰△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,连接FE、ED,BF的延长线交ED的延长线于点G,连接GC.
(1)求证:EF∥CG;
(2)若AC=![]() AB,求证:AC=CG;
AB,求证:AC=CG;
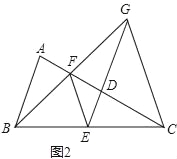
(3)如图2,若CG=EG,则![]() = .
= .
【答案】(1)证明见解析;
(2)证明见解析;
(3)![]()
【解析】
试题分析:(1)由点D、E分别是线段AC、BC的中点可得出DE为△ABC的中位线,根据中位线的性质即可得出∠CDE=∠A,进而可得出∠FDG=∠A,由此即可证出△ABF≌△DGF(ASA),根据全等三角形的性质即可得出BF=GF,即点F为线段BG的中点,再根据中位线的性质即可得出EF∥CG;
(2)过点C作CM⊥AB于点M,根据边与边的关系找出比例关系![]() =
=![]() =
=![]() ,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
(3)根据DE∥AB即可得出∠GEC=∠CBA,结合两三角形为等腰三角形即可得出△GEC∽△CBA,再根据相似三角形的性质即可得出![]() ,代入数据即可得出结论.
,代入数据即可得出结论.
试题解析:(1)∵点D、E分别是线段AC、BC的中点,∴DE为△ABC的中位线,
∴DE∥AB,∴∠CDE=∠A.∵∠CDE=FDG,∴∠FDG=∠A.
∵点F为线段AD的中点,∴AF=DF.
在△ABF和△DGF中,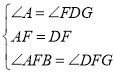 ,
,
∴△ABF≌△DGF(ASA),∴BF=GF,∴点F为线段BG的中点,
∵点E为线段BC的中点,∴EF为△BCG的中位线,∴EF∥CG.
(2)在图1中,过点C作CM⊥AB于点M.∵AC=BC,
∴AM=BM=![]() AB.∵AC=
AB.∵AC=![]() AB,
AB,
∴![]() =
=![]() =
=![]() .∵AF=
.∵AF=![]() AD=
AD=![]() AC=
AC=![]() AB,∴
AB,∴![]() =
=![]() =
=![]() ,
,
∴△BAF∽△CAM,∴∠AFB=∠AMC=90°,∴CF⊥BG.
∵点F为线段BG的中点,∴BC=CG,又∵AC=BC,∴AC=CG.
(3)∵DE为△ABC的中位线,∴DE=![]() AB,CE=
AB,CE=![]() BC=
BC=![]() AC,∵DG=AB,EG=DE+DG,
AC,∵DG=AB,EG=DE+DG,
∴EG=![]() AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
∴△GEC∽△CBA,∴![]() ,既
,既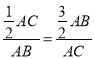 ,∴
,∴![]()
故答案为:![]() .
.