��Ŀ����
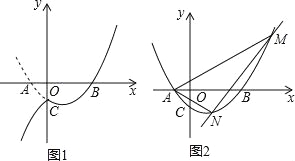
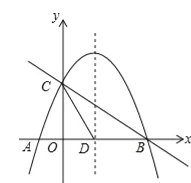
����Ŀ����ͼ��������y=��![]() x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
x2+bx+c��x�ύ��A��B���㣬��y�ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A����1��0����C��0��2����
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ��PCD����CDΪ���ĵ��������Σ�������ڣ�ֱ��д��P������ꣻ��������ڣ���˵�����ɣ�
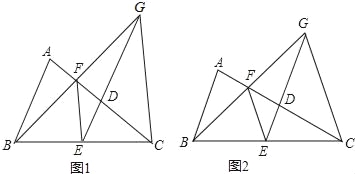
��3����Eʱ�߶�BC�ϵ�һ�����㣬����E��x��Ĵ������������ཻ�ڵ�F������E�˶���ʲôλ��ʱ����CBF�������������CBF������������ʱE������꣮
���𰸡���1��y=��![]() x2+
x2+![]() x+2��2�����ڣ�
x+2��2�����ڣ�![]() ����
����![]() ��
��![]() ������
������![]() ��
��![]() ����3��4��E��2��1��
����3��4��E��2��1��
��������
�����������1����A����1��0����C��0��2������y=��![]() x2+bx+c�з����鼴�ɣ�
x2+bx+c�з����鼴�ɣ�
��2�������CD�ij������������ٵ�CP=CDʱ���ڵ�DC=DPʱ�ֱ���⼴�ɣ�
��3�����ֱ��BC�Ľ���ʽ����E![]() ����F
����F![]() ���������κ��������ö��κ��������ʼ��ɽ�����⣮
���������κ��������ö��κ��������ʼ��ɽ�����⣮
�����������1����A����1��0����C��0��2������y=��![]() x2+bx+c��
x2+bx+c��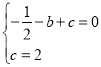 ��
��
���b=![]() ��c=2��
��c=2��
�������ߵĽ���ʽΪy=��![]() x2+
x2+![]() x+2��,
x+2��,
��2�����ڣ���ͼ1�У���C��0��2����D��![]() ��0����
��0����
��OC=2��OD=![]() ��CD=
��CD=![]() =
=![]()
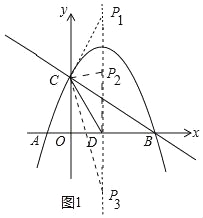
�ٵ�CP=CDʱ���ɵ�P1��![]() ��4����
��4����
�ڵ�DC=DPʱ���ɵ�P2��![]() ��
��![]() ����P3��
����P3��![]() ����
����![]() ��
��
��������������������P�������Ϊ![]() ����
����![]() ��
��![]() ������
������![]() ����
����![]() ����
����
��3����ͼ2�У�
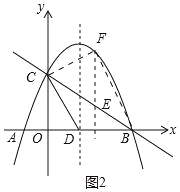
����������y=��![]() x2+
x2+![]() x+2����y=0ʱ����
x+2����y=0ʱ����![]() x2+
x2+![]() x+2=0�����x1=4��x2=��1
x+2=0�����x1=4��x2=��1
��B��4��0����A����1��0����
��B��4��0����C��0��2����ֱ��BC�Ľ���ʽΪy=��![]() x+2��
x+2��
��E![]() ��F
��F![]() ��
��
EF=![]() ��
��![]() =
=![]()
��-![]() ��0������m=2ʱ��EF�����ֵ2��
��0������m=2ʱ��EF�����ֵ2��
��ʱE��BC�е㣬
����E�˶���BC���е�ʱ����EBC������
���EBC������=![]() ��4��EF=
��4��EF=![]() ��4��2=4����ʱE��2��1����
��4��2=4����ʱE��2��1����

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�